Pas de définition académique justement parce que dans les programmes on ne nous donne quasiment jamais d'exercice où l'on serait souvent obligé de recourir à la méthode bourrin : développement puis réécriture en somme de carrés parfaits .
Pis dans les cours d'olympiades français ( Animaths, Soulami etc... ), ils n'ont jamais parlé d'inégalités sur les symétries ( plus généralement, ce qui se passe quand une séquence majore une autre, la preuve, aucun article en français sur Muirhead, aussi, rien que ce topic saute en deuxième place dans les résultats de recherche de Google pour "Inégalité de Muirhead" :ptdr: ), n'ont donc quasiment jamais besoin de développer de grosses expressions, et n'ont donc pas besoin d'introduire ce genre de notations .
Ce qui m'a poussé à lancer ce topic, c'est quand j'ai lu le post
http://www.mathlinks.ro/viewtopic.php?p=192974#192974 :
...
Another comment, the number one mistake I see with symmetric sum notation is people saying things like
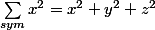
. THAT IS NOT TRUE. The whole point of symmetric sum is that you sum over all permutation regardless of the expression. So the correct form is
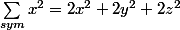
. You will see the reason behind this once you use Muirhead.
...
Donc je pense que, comme BenPi l'a suggéré, je vais utiliser la notation

pour désigner la somme sur toutes les

permutations des variables comme la majorité ( mathlinks entre autres ) le fait, et cela ne crée pas de confusion ( enfin, le symbole n'est pas utilisé pour désigner autre chose à ma connaissance ) .
PS : pour le

, c'est dans la "moyenne symétrique" ( symmetric mean comme l'a précisé l'auteur ) et pas dans la "somme symétrique", même si je ne vois pas son utilité vu que Muirhead dit que si
)
majore
)
, alors la "moyenne symétrique" des a_n est plus grande que celle des a'_n, car on simplifiera de toute façon par les

. ( mais bon c'est hors-sujet )

