La somme d'une série conditionnellement convergente
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 11 Mar 2012, 15:30
par Elerinna » 11 Mar 2012, 15:30
Soit
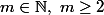
.
Montrer qu'il existe un réel x unique tel que la série :
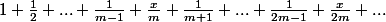
converge.
Calculer alors sa somme.
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 12 Mar 2012, 15:59
par MMu » 12 Mar 2012, 15:59
Elerinna a écrit:Soit
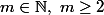
.
Montrer qu'il existe un réel x unique tel que la série :
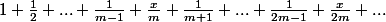
converge.
Calculer alors sa somme.
m+1}+...+\frac1 {(k-1)m+m-1}+\frac x{km}\right )=\frac{x-1+m}m\sum_{k=1}^n\fra 1k+\sum _{k=n+1}^{mn}\frac 1k)
La convergence implique
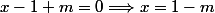
. D'autre part :
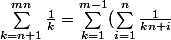)
Il est facile de voir que
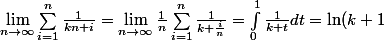-\ln(k))
Finalement la somme demandée est
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités