Réussite et e

[Rouvire]

Bonjour,

J'ai un jeu de n cartes. Elles sont numérotées de 1 à n. Je les bats et pose le paquet face cachée sur une table.
Je tire la 1ère carte du dessus et la repose à coté du paquet face découverte. Si c'est la carte n°1 j'ai perdu ma réussite, sinon je continue, je tire la carte du dessus du paquet et la repose face découverte sur la 1ère que je viens de tirer. Si c'est la carte n°2 j'ai perdu, sinon je continue et ainsi de suite. Je gagne ma réussite si j'arrive à retourner ainsi tout le paquet et que la dernière carte retounée n'est pas la n°n.

Quelle est la probabilité G de gagner en fonction du nombre de cartes?
J'ai G(1) = 0; G(2) = 1/2; G(3) = 2/6; G(4) = 9/24; G(5) = 44/120
Le dénominateur c'est n! mais le numérateur je ne sais pas. (quand on a n choses numérotées de 1 à n et qu'on les range dans n tiroirs numérotés aussi de 1 à n, avec une seule chose par tiroir, et qu'on veut qu'aucune chose se retrouve dans un tiroir qui aurait le même numéro, combien de façons a-t-on de faire?)

Quand n tend vers l'infini la probabilité G(n) tend vers 1/e (j'ai vu ça dans des livres et sans doute par valeurs inférieures?)

Maintenant quand j'ai gagné une réussite dans un sens j'essaye de faire le retour. Je prends le paquet qui est alors face découverte, je le laisse tel quel, et si la 1ère carte que je vois est la n°1 j'ai perdu, sinon je l'enlève, et si alors la carte que je vois et la n°2 j'ai perdu, sinon ...

Je crois que la probabilité de réussir un aller-retour tend vers 1/e² quand n tend vers l'infini (on dirait que les événements "gagner dans un sens" ou "gagner dans l'autre" sont ou deviennent indépendants quand n tend vers l'infini)

[beagle]

si n-1 choix par tiroir
, n tiroirs

(n-1)^n choix valables sur n^n cas possibles

alors [(n-1)/n]^n parait que cela va vers 1/e...

[Ben314]

Salut,
Pour la question de départ (où on ne fait que "l'aller"), c'est un grand classique des problèmles de dénombrement : parmi les n! (factorielle) permutations d'un ensemble à n élément, tu cherche combien il y en a qui n'ont pas de point fixes.
On appelle parfois de telles permutation des "dérangement".
A mon avis, le plus rapide pour obtenir la valeur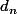 du nombre de dérangement consiste à écrire qu'une permution quelconque s'obtient (de façon unique) en choisissant éléments parmi les , puis un dérangement de ces éléments et en laissant les 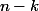autres fixés :
où désigne le coeff binomial (nombre de façon de tirer k éléments parmi n).
Si on note (resp. ) le vecteur colonne formés de (resp. ) et la matrice contenant les coeff binomiaux (=0 si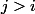) on a donc 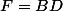c'est à dire .
Or un résultat archi classique est le fait que où .
On peut le démontrer soit directement en faisant le produit matriciel de par 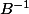ou bien, de façon bien plus jolie, en constatant que où est la matrice entièrement nulle sauf les termes en dessous de la diagonale qui valent 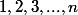et on en déduit que .
De toute façon, l'égalité dit que :
Ce qui montre clairement que tend vers .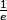

En ce qui concerne ta deuxième question, c'est à dire le nombre de permutations de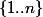 telles que, pour tout , et , je ne connais pas la réponse...

[Rouvire]

Merci Ben314

Je ne connaissais pas cette formule du nombre de dérangements (d'ailleurs je ne connaissais pas les "dérangements")



si je l'applique pour n=5

120 (1/1 - 1/1 + 1/2 - 1/6 + 1/24 - 1/120) = 44

ça marche