Request for help

[miso]

Bonjour tout le monde,

J'ai un petit souci à propos de la résolution de l'équation: exponentielle (-lamda) * (lamda + (lamda (carré))/2 + (lambda (cube))/6) = 1

Comment je peux obtenir lamda? Merci!

C'est l'approximation de la loi de Poisson!

[fatal_error]

slt,

tu peux pas avoir de valeur explicite (du moins avec les fonctions usuelles)
Par calcul numérique, tu peux t'en sortir avec une valeur approchée décente.

[miso]

Bonjour tout le monde,

J'ai un petit souci à propos de la résolution de l'équation: exponentielle (-lamda) * (lamda + (lamda (carré))/2 + (lambda (cube))/6) = 1

On m' a conseillé de prendre une valeur approchée au lieu de celle explicite (= 1).
Alors maintenant si je prends 0.999 au lieu de 1. Comment je peux procéder et comment je peux obtenir Lamda?
Comment je peux obtenir lamda? Merci!

[fatal_error]

donc déjà, lambda=1 pour valeur explicite, c'est faux. T'as qu'à vérifier, tu trouveras pas 1. pe pas loin, mais pas 1.

Ensuite, regarde la méthode de newton, par exemple, ou bien la dichtomie

[miso]

Bonjour,

Merci bien pour la réponse mais svp dis moi comment ça se fait la démarche? car je suis pas un mathématicien moi et je fais de l'informatique (prendre par exemple lamda = 0.999)!

Merci!

[fatal_error]

les informaticiens sont pas censes etre des billes en mathematiques. On attend pas d'eux de savoir resoudre une eq diff a la main, mais on attend au moins qu'ils soient capables de lire un algorithme et de l'appliquer.

Quest-ce que tu comprends pas dans la methode de newton?

[Anonyme]

équation: exponentielle (-lamda) * (lamda + (lamda (carré))/2 + (lambda (cube))/6) = 1
C'est l'approximation de la loi de Poisson!

Si ton équation est c'est à dire

Si tu traces les 2 fonctions définies par et avec appartenant à IR
tu vas pouvoir trouver une valeur approchée de ta solution

Au niveau algorithmique , il y a , de nombreux algorithmes différents qui permettent de calculer cette valeur approchée à près

Un algorithme très simple (pas très performant) est la méthode du balayage sur un intervalle donné
Mais compte tenu de la puissance des ordinateurs , tu ne recherches peut être pas forcément l'algo le plus performant !

Une valeur approchée de la solution est -3.49203

[Anonyme]

Si ton équation est c'est à dire

alors est une solution évidente

[miso]

Si ton équation est c'est à dire

alors est une solution évidente

Merci beaucoup, en fait c'est ça mon équation. Voila, très bien! :++:

[Anonyme]

Tout cela pour ca ?

[bablouze]

Tout cela pour ca ?

Salut ptitnoir, je m'incruste dans votre discussion pour poser une question sur un problème d'approximation d'une loi de Poisson,

Voici ma question:

Soit X une v.a suivant une loi de poisson de paramètre "lambda", comment peut-on montrer que: |P(X=k) pour k={2,3...} tend vers 0 à la vitesse "(lambda) ² " ???

indication: je sais qu'il faut utiliser la formule de taylor lagrange à l'ordre 1

Un grand merci d'avance!

[Anonyme]

Pour calculer une vitesse de convergence vers 0 d'une loi de Poisson quand k tend vers +infini
voici le calcul que je ferais


donc la vitesse de convergence de P(X=k) vers 0 quand k tend vers +infini est lente
( car la suite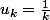 est une suite dont la vitesse de convergence est lente)


Question:
Peux tu préciser ce que tu entends par une vitesse en "(lambda) ² " ?

[bablouze]

Merci pour ta réponse,

Enfait l'énoncé que j'ai est mal posé, d' où le manque de données dans ma question, je m'en excuse.

Bon pour te faciliter la lecture de ce message assez long:
1) reformulation de la question
2) réponse à ta question sur la vitesse de CV
3) là où j'en suis dans la résolution de la question.


1)
_Soit k appartenant à {2,3,4,...}

_Soit X une v.a suivant une loi de Poisson de paramètre "lambda"

Il faut montrer que :

|P(X=k) tend vers 0 à la vitesse "(lambda)²" lorsque "lambda" tend vers 0.

(excuse si je ne l'avais pas précisé avant, mais même dans l'énoncé on ne le dit pas, mais c'est dans la logique du problème.)


2)
tendre vers 0 à la vitesse "(lambda)²" veut dire qu'on peut exprimer |P(X=k) en fonction de "(lambda)²" de telle sorte à ce que, dans cette expression, le terme "(lambda)²" soit celui qui tende le plus vite vers 0 lorsque "lambda" tend vers 0.

3)
Bon maintenant j'ai des éléments de réponse:
Pour k appartenant à {2,3,...}

|P(X=k) = 1 - |P(X=1) - |P(X=0)

= exp(-lambda) * [ exp(lambda) -1 -lambda]

et là on doit normalement utiliser la formule de Taylor-Lagrange pour déduire l'expression de |P (X=k) en fonction de lambda² qui nous permettra de conclure.


J'espère ne pas être trop lourd avec un message aussi long, mais voila j'ai essayé de t'éclaircir un peu les choses.


Merci beaucoup!!

[Anonyme]

Pour un k donné , comme

il faut faire le DL de cette expression quand tend vers 0 ?

Sais tu faire ce DL ?

[bablouze]

le (lambda)^k me bloque pour le DL..

[Anonyme]

ne t'en occupe pas et mets le en facteur

[bablouze]

ok, en faisant le DL(2) de l'exp on obtient:

|P(X=k)= [(1+lambda+(lambda²/2)+ o(lambda²)) * (lambda)^k ] / k!

le problème c'est qu'avec cette expression, je trouve que la proba tend vers 0 avec la vitesse (lambda)^k

[Kikoo <3 Bieber]

Merci beaucoup, en fait c'est ça mon équation. Voila, très bien! :++:

Salut à tous.
On a
Cas d'égalité si n est fini ?

[Anonyme]

je trouve que la proba tend vers 0 avec la vitesse (lambda)^k

Je suis d'accord avec ton résultat donc on n'obtient pas une vitesse en comme il est dit dans ton énoncé

Remarques:
Peut être que j'ai mal interprété ton énoncé et qu'il faut calculer "autre chose"

Par exemple :
P(X=k) avec k qui tend vers + infini et tend vers 0
ou
P(X=k+1)/P(X=k) pour un k donné quand tend vers 0
ou
P(X=k+1)/P(X=k) avec k qui tend vers + infini et tend vers 0

Je ne sais pas quoi dire d'autre....

[Anonyme]

Salut à tous.
On a
Cas d'égalité si n est fini ?

NON sauf pour