Répartir des points sur une ellipse
18 messages
- Page 1 sur 1
Répartir des points sur une ellipse
bonjour à tous,
je ne suis pas une star en mathématiques, d'où mon message sur ce forum.
J'ai besoin de répartir n points pour qu'ils soient équidistants sur le pourtour d'une ellipse (je ne sais pas si le terme de circonférence est approprié).
comment fais-je ??
prenons l'exemple avec 5 points et une ellipse dont le demi grand axe est 5, le demi petit axe est 3 et dont le centre serait en (0,0). Quels seraient les angles de chacun de ces points avec l'horizontale passant par l'origine ??
ça serait un cercle, je diviserait 360° par 5, mais pour une ellipse, j'ai besoin d'aide !!!
Merci à tous ceux qui prendront le temps de me lire et peut-être de répondre !!!
THE SENSEI
je ne suis pas une star en mathématiques, d'où mon message sur ce forum.
J'ai besoin de répartir n points pour qu'ils soient équidistants sur le pourtour d'une ellipse (je ne sais pas si le terme de circonférence est approprié).
comment fais-je ??
prenons l'exemple avec 5 points et une ellipse dont le demi grand axe est 5, le demi petit axe est 3 et dont le centre serait en (0,0). Quels seraient les angles de chacun de ces points avec l'horizontale passant par l'origine ??
ça serait un cercle, je diviserait 360° par 5, mais pour une ellipse, j'ai besoin d'aide !!!
Merci à tous ceux qui prendront le temps de me lire et peut-être de répondre !!!
THE SENSEI
Alors tu peux utiliser les formules de la longueur de la courbe entre les paramètres t1 et t2
=\int_{t1}^{t_2} \sqrt{x'^2(u)+y'^2(u)}du)
avec ton équation paramétrique de l'ellipse:
x(t)=a cost
y(t)=b sint.
Tu calcules ainsi la valeur approchée de la longueur de l'ellipse: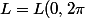) , et dans ton exemple tu cherches numériquement les paramètres tels que
, et dans ton exemple tu cherches numériquement les paramètres tels que
=\frac L n) (en supposant que tu places le premier point à droite.)
(en supposant que tu places le premier point à droite.)
=\frac L n) ...
...
Attention: les paramètres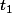 ... ne représentent pas l'angle que tu cherches, mais l'angle au centre du cercle dont l'ellipse est image par une affinité. Cela te rappelle quelque chose? :happy2:
... ne représentent pas l'angle que tu cherches, mais l'angle au centre du cercle dont l'ellipse est image par une affinité. Cela te rappelle quelque chose? :happy2:
avec ton équation paramétrique de l'ellipse:
x(t)=a cost
y(t)=b sint.
Tu calcules ainsi la valeur approchée de la longueur de l'ellipse:
Attention: les paramètres
Désolé si je t'ai fait un peu peur...
la longueur de la courbe entre les paramètres t1 et t2 est
=\int_{t1}^{t_2} \sqrt{a^2 \sin^2(u)+b^2 \cos^2(u)}du)
avec ton équation paramétrique de l'ellipse:
x(t)=a cost (a demi grand-axe)
y(t)=b sint (b demi petit-axe)
Sais-tu calculer une valeur approchée d'intégrale avec une calculette?
Autre remarque, quand on obtient un paramètre t1 par exemple (voir mon post précédent), cela ne fournit pas l'angle que tu cherchais mais plutôt les coordonnées du point de l'ellipse:
x=a cos(t1)
y=b sin(t1)
la longueur de la courbe entre les paramètres t1 et t2 est
avec ton équation paramétrique de l'ellipse:
x(t)=a cost (a demi grand-axe)
y(t)=b sint (b demi petit-axe)
Sais-tu calculer une valeur approchée d'intégrale avec une calculette?
Autre remarque, quand on obtient un paramètre t1 par exemple (voir mon post précédent), cela ne fournit pas l'angle que tu cherchais mais plutôt les coordonnées du point de l'ellipse:
x=a cos(t1)
y=b sin(t1)
je viens d'essayer tes valeurs, je confirme, c'est parfait !!!
par contre, j'suis vraiment désolé, mais je n'arrive pas à comprendre ta formule : quand tu me parles de la longueur de la courbe entre les paramètres t1 et t2, c'est quoi le u dans la formule ??
tu pourrais me réecrire cette formule en mettant mes valeurs dedans, ça m'aiderait à comprendre ?
par contre, j'suis vraiment désolé, mais je n'arrive pas à comprendre ta formule : quand tu me parles de la longueur de la courbe entre les paramètres t1 et t2, c'est quoi le u dans la formule ??
tu pourrais me réecrire cette formule en mettant mes valeurs dedans, ça m'aiderait à comprendre ?
Dans ton exemple, le demi-grand axe est 5 (a=5) et le demi petit-axe est 3 (a=3).
Cela donne une longueur totale :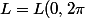=\int_{0}^{2\pi} \sqrt{25 \sin^2(u)+9 \cos^2(u)}du)
Le u est une variable muette. Tu peux écrire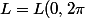=\int_{0}^{2\pi} \sqrt{25 \sin^2(x)+9 \cos^2(x)}dx) si tu préfères.
si tu préfères.
Cette intégrale représente l'aire en dessous de la courbe de la fonction
+9 \cos^2(x)}) de 0 à
de 0 à  .
.
Tu peux l'approcher par la méthode des rectangles, des trapèzes...
Tu n'as jamais vu une intégrale?
Cela donne une longueur totale :
Le u est une variable muette. Tu peux écrire
Cette intégrale représente l'aire en dessous de la courbe de la fonction
Tu peux l'approcher par la méthode des rectangles, des trapèzes...
Tu n'as jamais vu une intégrale?
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
