Régulation des prix

[ppollopp]

Bonjour à tous,

Je suis un petit peu bloqué dans la recherche d'une formule qui me tracasse depuis un petit temps :)
Je viens donc demander un peu d'aide aux maitres :P

Je vous explique donc mon problème :

J'essaie de mettre au point un algorithme de régulation des prix.
Je vous explique plus en détail.
Dans l'environnement en question, il existe 3 ressources différentes.
Appelons les bois, fer et or.
Chaque agents possèdent une certaine quantité de chacune des ressources.
Dans le système en question, il existe une banque centrale, qui permet à un agent d'échanger une certaine quantité de ressources contre une certaine quantité d'une autre ressource.

Le taux de change que propose la banque devrait se réguler automatiquement en fonction de l'offre et la demande !
Exemple.
Un agent a besoin de fer et a beaucoup de bois, il contacte alors la banque qui lui propose une certaine somme de fer en échange de son bois.
Mais, si beaucoup d'agents se mettent a avoir le même comportement, c'est a dire vendre du bois contre du fer, la banque va adapter ses taux de change en demandant plus de bois pour une même quantité de fer.
Et de même, la banque offrira plus de bois a quiconque lui fournira du fer.

Donc dans notre exemple, si au départ la banque fourni 1 unité de fer contre 3 unités de bois, si la demande de fer augmente, elle pourrait demander 5 unité de bois contre une unité de fer.
Ce que j'essaie de mettre au point est un algorithme qui calcule les différents taux de change en fonction du comportement des agents et ce en temps réelle.

Idée de départ.

Dans mon idée de départ, la banque centrale contiens une certaine
quantité de chaque ressource, au même titre que les agents.
Nommons ces quantités :
B = Quantité de bois que possède la banque centrale.
F = Quantité de fer que possède la banque centrale.
Or = Quantité d'or que possède la banque centrale.

Mon algorithme fonctionne comme ceci :
Dans notre exemple, un agents désire vendre 100 tonnes de bois et veux
acquérir du fer en échange.
La banque centrale dispose des ressources suivantes :
B=2000, F=1000 et Or=300
Elle calcule son taux
De change de la manière suivante: F/B.
Donc en échange des 100 unités de bois, elle va fournir F/B * 100
unités de fer, c'est a dire, 1000/2000 * 100 = 50 unité de fer.
Après la transaction, la banque centrale dispose des ressources
suivantes: B=2100, F=950 et Or=300.
Si un autre agent ou le même désire faire la même transaction, le taux
de change sera maintenant de 950/2100 et la banque ne proposera plus
que 45 de fer en échange de 100 unités de bois.
Le problème c'est qu'il ne faut surtout pas que la banque centrale
vende a perte ! Au contraire, elle devrait même prendre une petite
commission sur chaque transaction.

Mon algorithme me plait bien mais il a un problème...
Ce problème se pose lorsque les réserves de la banque sont proches de la quantité que veut échanger un agent.
Petit exemple, la banque possède 100 unités de bois et 50 de fer.
Un agent vient vendre 80 unités de bois, la banque lui fourni donc en échange 40 unités de fer (50/100 * 80). Si notre agent revend instantanément le fer qu'il vient de recevoir, la banque va lui donner 720 unités de bois !!! (180/10 * 40)
Donc de un la banque a vendu a perte, son stock de bois étant de -540
et de deux n'importe quel agent peut devenir immensément riche en
répétant la manipulation.

J'essaie de faite en sorte que ce ne soit pas possible mais je ne parviens pas à trouver la bonne modification à mes équations...
Pour bien faire, il faudrait que quand un agent refasse juste l'inverse d'une transaction qu'il vient de faire, il se retrouve avec ses quantités de départ voir un peu moins mais surtout pas plus !

Un second problème est que avec mon implémentation actuelle, si la banque prend une commission a chaque fois, les stocks de la banque vont tendre vers l'infini !
Et comme c'est assez délicats de stoquer de très très grand nombres dans une base de données il faudrait trouver une solution.

Un tout grand merci d'avance pour votre aide

[fatal_error]

yo,

jme lance.
soit le nombre d'unités de fer à la banque.
Soit le nombre d'unités de bois à la banque.
on définit le poids par

on définit l'évaluation d'un élément du type par

cette pondération permet d'avoir la valeur de x, répondant à peu près à la loi de l'offre et de la demande.
Si est en proportion inférieure par rapport à , alors on évalue x comme plus important.

Maintenant la fonction.
Il arrive une quantité de bois .
Au change on récupère une certaine quantité x qu'on veut définir.
L'idée c'est d'évalue la quantité obtenue, et de faire en sorte que son évaluation soit inférieure à la quantité en entrée (avant le change).
cela équivaut à écrire : (1)
On pose
on remarque déjà que ce que satisfait déjà l'inéquation.
Ensuite, on aimerait trouver x, tel que f(x)>0 et 0<x<c_1
ca correspond à une étude de fonction que jai pas courage de faire.

moyennant les ptites boulettes bien sûr...

[fatal_error]

re,

ok, je pense avoir une solution .
donc on reprend les notations ci-dessus.
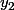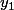Il arrive unités (donc de type de ). On veut trouver les qu'on récupère au change.
Donc on a avant le change une évaluation qui vaut

On en particulier (1)
next, on retranche x unités à et il reste respectivement et dans la banque
l'évaluation apres change vaut :

on étudie la fonction
on montre qu'elle est croissante de 0 à x_1, et de x_1 à l'infini. (deux intervalles car est valeur interdite)
En particulier, v(0)=0, et
cela signifie qu'il existe un x_0, tel que ou pas, (si ce nest que les quantités de la banque sont positives, et les données en entrée aussi), ca signifie qu'on peut réitérer cette étape plein de fois.

Idéalement, il faudrait qu'on puisse montrer qu'en retrant dans le système en tant que donné de , on obtienne 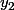en sortie, mais bon...
On remarque aussi qu'on peut retirer une certaine quantité lors de la transaction en rendant moins d'unités que . En effet, la fonction d'évaluation etant croissante, pour qui traduit bien le fait que le gus s'est fait niquer au change.
Apres tu peux essayer de paramétriser de combien il se fait entuber. Tu peux imaginer 5% de l'évaluation en entrée, et convertir ca en nombre d'unités correspondantes dans l'autre matiere (sous reserve de ne pas rendre une ressource négative!)

[fatal_error]

jen ai profité pour faire un ptit script voire si ca marchait. Ca a l'air.
test 1: on met 80 en entrée, on recupère s. on met 60 en entrée. On veut récupérer moins que s.
test 2: on met 80 en entrée, on récupère s. On met s en entrée, on récupère moins que 80
jenquille ca dans une boucle au lieu de 80.

Il reste à vérifier la fonction d'évaluation pour une dimension plus grande que 2. Mais jpense qu'on peut garder la somme. Ca représente le ratio de la quantité présente dans la banque.

voici le source code octave
fais un change, inType prend ses valeurs dans les indices de la bank. ex : inType = 1, c'est bois, 2, c'est fer.

Code: Tout sélectionner

function x=change(y_2, inType, outType)
  global bankRessources;
  bankRessources
  total = sum(bankRessources);
  x_1 = bankRessources(outType);
  x_2 = bankRessources(inType);
  C_2 = y_2*total/x_2;
  delta=y_2*total/x_2;
  r = x_1+x_2+y_2;
  trinomeX2=1;
  trinomeX=-(r+delta);
  trinomeC=delta*x_1;
  [s_1, s_2] = eqSolver(trinomeX2, trinomeX, trinomeC);
  if(00)
    x_1=(-b-sqrt(delta))/(2*a);
    x_2=(-b+sqrt(delta))/(2*a);
  else
 
  end 
end


le main

Code: Tout sélectionner

clear;
bank;
oldChanged=0;
oldRetrieved = 0;
for i=1:5:100
changed=change(i,2,1);
retrieved=change(changed,1,2);
  if(oldRetrieved>retrieved)
    disp('fail')
  end
  if(oldChanged>changed)
    disp('fail')
  end
oldRetrieved = retrieved;
oldChanged = changed;
end


[fatal_error]

c'est encore moi!

apres entretien avec un coloc, il a bien pointé du doigt le probleme suivant :
si, pour une raison ou pour une autre, on a x_1=0, alors on a une pondération infinie, cqui est pas bon.

La solution qu'il propose, c'est de décomposée en la somme
et de réaliser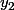 fois la transaction (dans le concept)
Apres, il y a les problemes d'arrondis, donc il faut s'arranger pour filer suffisamment de "1" pour avoir l'équivalent d'une ressource, et ainsi de suite.

mais personnellement, jtrouve ca un peu space...

[fatal_error]

c'est encore moi :we:

alors, pour le probleme de la pente infinie, on peut sen sortir en divisant par x_1+1 au lieu de x_1 dans le cas ou x_1 vaut 0. il faut vérifier pour les ptits nombres, mais sinon, ca roule.

Pour le poste précédent, voici une approche un peu moins bête:
on définit la suite a_n comme la quantité de bois à la nieme transaction. a_0 etant la quantité avant transaction.
on a donc pour 50 bois 50 transactions de valeur 1.
Soit :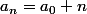
pour b_n, même chose mais pour le fer, on définit

avec si la ressource qu'on apporte est du type de a_n (genre si a_0 vaut 50, et b_0 qui vaut 100, alors la ressource de type a_n vaut plus que celle de type b_n, donc on retranche plus de b_n ce qui est le cas ici).
cette equation se reecrit

avec
par récurrence, il vient

les termes du produit se simplifie entre numérateur et dénominateur du précédent, il reste donc

now, il reste le probleme du manque dune ressource, on introduit alors la relation
, ce qui signifie qu'on fait apparaitre une ressource virtuelle dans la banque.Ca a pour effet de rendre la ressource "moins rare". cela se répercute sur le a_0 et le terme b_n devient des lors. Cet écart fausse notamment la donne si b_0 et a_0 sont du même ordre que 1 (l'offset que nous ajoutons). mais on voit que modifier a_0 par un terme constant n'est pas gênant!
ou encore


au début j'étais sceptique, mais ce mécanisme est le même (dans l'idée) que celui que j'ai présenté précédemment, sauf qu'on est plus précis, c'est un peu comme si on faisait une transaction en suivant l'évolution du marché! (a prendre avec des pincettes quand même :we: )

il ne reste plus qu'à prendre le ceil de b_n et c'est réglé (b_n etant la quantité qui reste dans la banque, on va éviter de se faire baiser par l'arrondi!):)

[ppollopp]

Waow !

Je te remercie vraiment pour tout le temps que tu me consacres, ça me fait énormément plaisir :)

Je sens que je vais devoir lire tout ça calmement afin d'être sur de bien tout comprendre ;)

Je reviens très vite te dire ce que j'en pense et ce que je n'ai pas très bien compris ;)

Encore un tout grand merci en tout cas !

Ppollopp.