OK pour le début.
Pour le dernier return : revenons à la définition de la suite : la relation de récurrence est
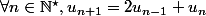
C'est-à-dire, comme
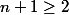
, on calcule les termes à partir du rang 2 en additionnant le précédent avec le double du précédent du précédent. On peut donc écrire à la place
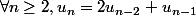
Donc, dans le programme Python : si

on a le return, si

on a le return, sinon on est dans le cas

, donc le return, c'est 2*u(n-2)+u(n). Ce qui donne (attention aux indentations
def u(n) :
if n==0:
return 3
elif n==1:
return 1
return 2*u(n-2)+u(n-1)
(Ce principe d'une fonction qui s'appelle elle-même s'appelle "récursivité". Cela fonctionne parce qu'il y a une condition d'arrêt, qui est ici n==0 ou n==1, la fonction ne s'appelle pas elle-même dans ce cas)
Par exemple, si on veut calculer u(4) :
- comme 4>=2, on va appeler u(2) et u(3) pour calculer 2*u(2)+u(3)
- pour u(2), on va appeler u(0) et u(1)
- u(0) renvoie 3
- u(1) renvoie 1
- on a donc calculé pour u(2) : 2*3+1=7
- pour u(3) on va appeler u(1) et u(2)
- u(1) renvoie 1
- u(2) va appeler u(0) et u(1)
- u(0) renvoie 3
- u(1) renvoie 1
- on a donc calculé pour u(2) : 2*3+1=7
- on a donc calculé pour u(3) : 2*1+7=9
- On a donc calculé pour u(4) :2*7+9=23
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
