Prove that AMCD is a cyclic quadrilateral

[brhum.moh]

[mathelot]

Démontrer que les points A,M,C,D sont cocycliques ainsi que les points B;M,C,V ou

Démontrer que le quadrilatère AMCD est inscriptible ainsi que le quadrilatère BMCV .


contexte: se reporter à une démonstration du théorème de Pythagore
par les aires , dûe à Euclide.

[chan79]

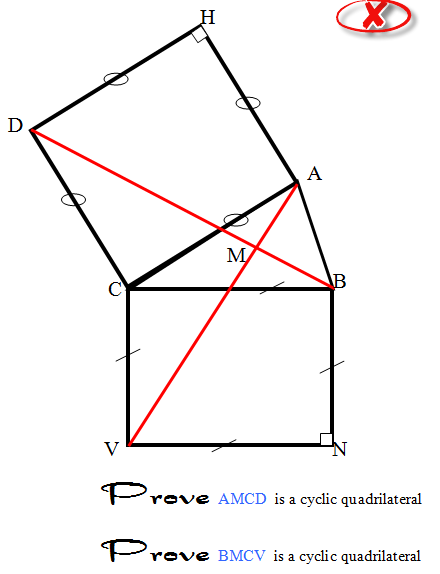
Montrer que les deux segments rouges sont perpendiculaires. (il suffit de chercher l'image de [AV] par la rotation de centre C qui transforme A en D).
Ensuite, les différents angles droites permettent de conclure.

[mathelot]

la rotation affine de centre C et d'angle de mesure envoie le point D sur A
et B sur V:
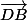
cette rotation affine s'appuie sur la rotation vectorielle telle que donc et sont orthogonaux (=perpendiculaires) ce qui fait
que les points D,C,M,A sont cocycliques, situés sur le cercle de diamètre [AD].