Progression/suite

[cestpatou]

Bonjour,

J'ai fait un concours mathématique aujourd'hui et cette question m'a principalement laissé perplexe. Pouvez-vous m'aider à trouver comment résoudre cette question? J'ai mis la question plus bas. Je dois spécifier que dans ce concours, on a pas le droit à l'ordinateur ou à une calculatrice ^^".

Merci beaucoup !


Les termes numéro 1, 2, 3 et 4 d'une suite sont respectivement 13^0, 13^1, 13^2 et 2014. Ensuite, chaque terme de la suite est toujours égal à la somme des quatre précédents. Le terme numéro 5 de la suite est ainsi 13^0 + 13^1 + 13^2 + 2014 = 13^3. Quel est le nombre de chiffres du terme numéro 2014 de la suite? Si nécessaire, log étant le logarithme en base 10, on prendra 0.285 pour log(1.928) et 0.942 pour log(8.748).

[Ben314]

Salut,
Je sais pas trop quelles connaissance tu as (en particulier sure les suites récurentes), mais si tu as un peu de "bouteille", tu doit savoir qu'une suite dont un terme est la somme des 4 précédent, c'est une combinaison linéaire des 4 suites géométrique de raison q où q est une des 4 racine de .
Ca doit pas être trop dur de vérifier (même sans calculettes) qu'il y a deux racines réelles, une dans ]-1,0[ et l'autre Q dans ]1,2[ et deux racines complexes de module <1 ce qui montre que Un est de plus en plus proche de a.Q^n.
Reste à trouver Q et a.
Pour avoir une bonne approximation de Q, je pense que le plus simple est d'écrire que :
donc
Q étant proche de 2, il est trés proche de et encore plus proche de ... (là, il faut se taper à la main 3 ou 4 calculs d'inverse et de puissance 4em pour avoir l'approximation qui était évidente vu les "indics" de l'énoncé)

Aprés, concernant le facteur a de a.Q^n, je sais pas trop ce qui est le plus simple... (faisable à la main), mais d'un autre coté, vu qu'on demande uniquement le nombre de chiffre de U2014, il n'y a pas besoin d'un encadrement génial de a (contrairement à Q qui va apparaitre à la puissance 2014...)

[cestpatou]

Mes connaissances sur les séries/suites sont très limitées. J'ai déjà suivi un cours là-dessus mais c'était jadis !

Pour ce qui est de ta première formule, doit-on ignorer le fait que X ne vaut pas 13?

Pour ce qui est des racines réelles, comment peux-tu affirmer que c'est entre ]1,2[ ? Comment factorises-tu cela pour savoir que c'est entre 1 et 2? Est-ce que c'est une connaissance de base à acquérir?

Sinon à partir de Q approximé à 1.928, on tombe ensuite à 1.928^2013 (puisque le premier terme est q^0=1)? Si oui, le reste est facile en transposant dans les données du problème pour transformer en logarithme et faire le calcul de 2013* log(1.928) ce qui donne approximativement 573.9 donc 574 chiffres?

[Ben314]

Pour faire "vite fait" un petit bout de théorie, lorsque tu as une suite définie par "récurence linéaire" comme ici où (en oubliant totalement de regarder les valeurs de départ)
Tu commence par regarder s'il n'y aurait pas des suites "simples" qui vérifient .
Si tu "teste" une suite géométrique de raison q, il est clair (ou façile à vérifier si ce n'est pas clair) qu'elle vérifie la formule ssi q est une solution de l'équation .
Normalement (i.e. à quelques exeptions prés...) une telle équation à 4 solutions dans C ce qui fourni 4 valeurs possible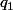 , , 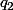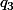et 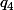pour la raison de la suite.
Ensuite, il est clair (ou façile à vérifier) que toutes les suites de la forme vérifient , quelque soient la valeur des constantes (à priori complexes) a,b,c et d.

Après, on ressort de dessous le mouchoir où on les avait mise les "condition initiales" U_1=? , U_2=? , U_3=? et U_4= ? qui permettent (via la résolution d'un système linéaire de 4 équations à 4 inconnues) de déterminer a,b,c et d.

Donc, pour revenir à tes question, le fait que la 4em valeur ne soit pas 13^4, on s'en fout complètement en ce qui concerne la recherche de Q (et des autres solutions de l'équation) vu que l'équation ne provient QUE de la formule de récurence et pas des valeurs initiales.

Aprés, pour déterminer à la main où sont (approximativement) situées les solution de (à la machine, c'est fastoche avec wolfram), j'utiliserais le fait que, pour 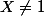, donc que l'équation équivaut à trouver les racines (autres que 1) du polynôme .
Polynôme dont le signe de la dérivé est super simple à évaluer et cela permet d'avoir les variation de P et donc de localiser les racines réelles.
Concernant les 2 racines complexes, là, je sais pas ce qu'il y a de simple (i.e. sans utiliser la théorie de Cauchy et les résidus) pour montrer qu'elle sont de module oo et le 4em vaut Q=1.928 et c'est pas en regardant les premiers termes qu'on trouvera la constante qui va devant le Q^n (sans connaitre assez précisément les autres racines...)

En fait il y a uniquement celui associé à la racine proche de 2 qui nous intéresse, mais je vois pas comment l'estimer, même approximativement et il joue un (petit) rôle dans le résultat final...

Donc je soupçonne une "astuce" lié aux valeurs spéciales des 4 premiers termes (tout ce que je raconte ne dépend absolument pas de ces 4 valeurs là).
Mais par contre, il est totalement évident que la plus grande des racine de l'équation joue forcément un grand rôle dans toute solution vu que 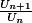tend vers cette valeur là.