Produit vectoriel de dimension N

[BUD]

Bonjour à tous,

je voulais savoir comment on calculait un produit vectoriel avec des vecteurs de taille quelconque.

Merci d'avance.

BUD

[leon1789]

Tu es dans ? Il te faut n-1 vecteurs en donnée pour calculer leur produit vectoriel, c'est bien ça ?

[leon1789]

Avec un coup de déterminant, on le généralise en tant qu'application -linéaire alternée,
dont le résultat est orthogonal aux vecteurs donnés ,
(et tel que quand on travaille sur R.)
qui "échange" les éléments de la base canonique ...

[leon1789]

Non, tu ne délires pas. Il est clair que pour n>3, on a :ptdr: Ce que je veux dire par là, c'est que , c'est petit en dimension et qu'il y a pas mal de trucs qui se simplifient en dim 3...

Cela étant, quel que soit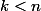 , on peut définir une généralisation moulinant sur k vecteurs, et produisant une application (n-k)-linéaire alternée (valant la fonction nulle si et seulement si les k vecteurs sont liés), valant 0 dès qu'un de ses arguments est dans l'espace engendré par les k vecteurs. Et dans le cas particulier où n-k=1 (par exemple 2=k < n=3), cela définit un vecteur tel que...

Bien sûr, mais le produit de 2 vecteurs dans ce cadre n'a pas de sens...

Il faudrait savoir précisément ce qu'on veut généraliser, quels résultats on veut retrouver après la généralisation...