De produit en somme
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
par manoa » 13 Déc 2011, 23:20
Salut à tous!
En bidouillant un peu avec les primitives et la dérivé,je suis tombé sur un résultat que j'ai essayer de généraliser,et j'ai voulu savoir si un truc pareil existe,vu que j'essaye dapprofondir un peu mes connaissances en sommes télescopiques,et tous ce qui de transformer un produit en somme.(si vous pouviez me passer quelques pistes sur quoi travailler (la télescopie en général) ça serait sympa ^^)
Alors voici mon 'tit résultat :
Pour a,b,c,d,
réels différents de 0 et pour tous x de R-{(-b/a);(-d/c)} on pose :
=\frac{\alpha}{(ax+b)(cx+d)})
On a
=\frac{\alpha}{ad-bc}(\frac{a}{ax+b}-\frac{c}{cx+d}))
et donc les primitives de f s'écrivent sous forme:
+k)
avec
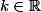
(":" pour la valeur absolu)
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
par Mortelune » 13 Déc 2011, 23:42
Bonsoir, tu eux essayer de regarder du côté de la décomposition en éléments simples. (C'est ce que tu as fais pour f)
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
par manoa » 14 Déc 2011, 14:34
Ah merci Mortelune,c'est bien ce que je cherchais :we:
Sinon pour les sommes télescopiques..pouvez vous me donner quelques mots clés pour approfondir mes recherches ? je ne trouve pas grand chose :triste:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
