Problème de résolution
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 17 Juin 2015, 16:52
par ludexige » 17 Juin 2015, 16:52
Bonjour à tous
Je suis bloqué avec une formule
h=2*fz*racine((a/D)*(1-(a/D)))
J'aimerai savoir à quoi est égal a
merci

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 17 Juin 2015, 18:09
par fatal_error » 17 Juin 2015, 18:09
hello,
h=2*fz*racine((a/D)*(1-(a/D)))=>
h^2=4fz^2(a/D)*(1-(a/D))<=>
h^2/4fz^2=(a/D)*(1-(a/D)
soit K=h^2/4fz^2
K=(a/D)*(1-(a/D)<=>
K=a/D-a^2/D^2<=>
K*D^2=aD-a^2<=>
a^2-aD+KD^2=0<=>
trouver a est facile.
il reste à vérifier que le a que tu choisis satisfait ton eq de départ.
la vie est une fête

-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 17 Juin 2015, 18:25
par ludexige » 17 Juin 2015, 18:25
fatal_error a écrit:hello,
h=2*fz*racine((a/D)*(1-(a/D)))=>
h^2=4fz^2(a/D)*(1-(a/D))
h^2/4fz^2=(a/D)*(1-(a/D)
soit K=h^2/4fz^2
K=(a/D)*(1-(a/D)
K=a/D-a^2/D^2
K*D^2=aD-a^2
a^2-aD+KD^2=0
trouver a est facile.
il reste à vérifier que le a que tu choisis satisfait ton eq de départ.
Merci
en faite ce que je veux c'est à par rapport au reste
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 09:34
par ludexige » 23 Juin 2015, 09:34
ludexige a écrit:Merci
en faite ce que je veux c'est à par rapport au reste
Je n'arrive pas à isoler le a

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Juin 2015, 09:51
par ampholyte » 23 Juin 2015, 09:51
ludexige a écrit:Je n'arrive pas à isoler le a
Bonjour,
Il te suffit de résoudre l'équation du second degré que fatal_error a extrait de ton expression et de choisir la bonne solution.
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 10:01
par ludexige » 23 Juin 2015, 10:01
ludexige a écrit:Merci
en faite ce que je veux c'est à par rapport au reste
Je n'arrive pas à isoler le a
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 10:02
par ludexige » 23 Juin 2015, 10:02
ludexige a écrit:Je n'arrive pas à isoler le a
Comment faire pour écrire a = ............
En faite j'aimerai calculer le a
Merci

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Juin 2015, 10:04
par ampholyte » 23 Juin 2015, 10:04
Est-ce que tu sais résoudre une équation du type :
ax² + bx + c = 0 ?
Si tu sais faire cela tu sais résoudre l'équation de fatal_error.
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 10:15
par ludexige » 23 Juin 2015, 10:15
ampholyte a écrit:Est-ce que tu sais résoudre une équation du type :
ax² + bx + c = 0 ?
Si tu sais faire cela tu sais résoudre l'équation de fatal_error.
Je cherche car c'est loin
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 10:44
par ludexige » 23 Juin 2015, 10:44
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 18:49
par ludexige » 23 Juin 2015, 18:49
Déjà je vois pas le rapport entre
a^2-aD+kd^2
Et
ax^2+bx+c

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Juin 2015, 18:54
par ampholyte » 23 Juin 2015, 18:54
x est simplement une inconnue, cela aurait pu être y, a, toto, jules, ...
Donc quand tu as :
Ax² + Bx + C = 0
on aurait pu écrire :
Aa² + Ba + C = 0
Donc dans ton exemple, en posant :
A = 1
B = -D
C = kd²
Tu retombes sur ton équation.
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 19:11
par ludexige » 23 Juin 2015, 19:11
ampholyte a écrit:x est simplement une inconnue, cela aurait pu être y, a, toto, jules, ...
Donc quand tu as :
Ax² + Bx + C = 0
on aurait pu écrire :
Aa² + Ba + C = 0
Donc dans ton exemple, en posant :
A = 1
B = -D
C = kd²
Tu retombes sur ton équation.
D'après ce que tu écris Je trouve un delta <0 donc pas de résultats
Delta=-D-4kD^2
Avec k=h^2÷(4fz^2)
D=16
h=0.02
Fz=0.07
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 19:12
par ludexige » 23 Juin 2015, 19:12
Normalement mon a devrait être égale à ~0.3

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Juin 2015, 19:44
par ampholyte » 23 Juin 2015, 19:44
Attention ton delta est faux :
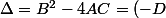^2 - 4 * 1 * kD^2)
-
ludexige
- Membre Naturel
- Messages: 11
- Enregistré le: 17 Juin 2015, 16:42
-
 par ludexige » 23 Juin 2015, 20:12
par ludexige » 23 Juin 2015, 20:12
Je pense avoir trouver grâce à toi
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
