Comment peut t'on resoudre celle ci ? S'il vous plait !
https://drive.google.com/file/d/0By8MET ... p=drivesdk
Probleme limites en math
4 messages
- Page 1 sur 1
Re: Probleme limites en math
Bonjour,
On peut faire le changement de variable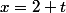 pour se ramener en 0, et factoriser le dénominateur par
pour se ramener en 0, et factoriser le dénominateur par  . On obtient
. On obtient }{\sqrt 2 (\sqrt{1+\dfrac{t}{2}}-1)}) . Puis on utilise les équivalents en 0 :
. Puis on utilise les équivalents en 0 :
 \sim \dfrac{\pi}{2}t)
} \sim \dfrac{t}{4}) .
.
Sauf erreur, on trouve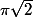 .
.
On peut faire le changement de variable
Sauf erreur, on trouve
Re: Probleme limites en math
Najib12 a écrit:Comment peut t'on resoudre celle ci ? S'il vous plait !
https://drive.google.com/file/d/0By8MET ... p=drivesdk
Salut,
Par l'Hopital
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Probleme limites en math
salut

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
