Problem 2
2 messages
- Page 1 sur 1
par Ben314 » 12 Juin 2014, 18:06
Salut,
(n+2)...(n+500)}{500!}=\frac{(n+500)!}{n!\times500!}={n+500\choose 500}\)
(coeff. binomial)
Si, pour
premier, on note )
la valuation -adique de l'entier 
, c'est à dire l'exposant de dans la décomposition de en produit de facteurs premiers, on voit facilement que =\sum_{k\geq 1}\lfloor\frac{m}{p^k}\rfloor\)
où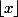 
désigne la partie entière du réel 
.
Donc=\sum_{k\geq 1}\Big(\lfloor\frac{n+500}{p^k}\rfloor-\lfloor\frac{n}{p^k}\rfloor-\lfloor\frac{500}{p^k}\rfloor\Big)\)
ce qui signifie que ne divise pas 
ssi 
pour tout 
ce qui signifie que, lorsque l'on ajoute 
et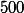 
en base , l'addition ne doit contenir aucune retenue.
Si, par exemple, on prend pour le produit des nombres premiers inférieurs à 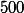en mettant sur chaque nombre premier un exposant 
tel que 
alors il est clair que la condition çi dessus sera vérifiée.
Il existe surement de plus petit tels vu que, pour qu'il n'y ait pas de retenues, il n'est pas nécessaire (mais uniquement suffisant) que les derniers chiffres de soient des zéros.
Si, pour
Donc
Si, par exemple, on prend pour
Il existe surement de plus petit tels
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :