Je viens de tomber sur une démonstration qui m'a ébloui alors je ne résiste pas à vous poser la question.
La question est :
On prend 2 nombres au hasard, quel est la probabilité pour qu'ils soient premier entre eux (donc pas de diviseur commun).
Par exemple s'ils sont déjà tout deux pairs ils ne sont pas premier entre eux.
Même si vous ne trouvez pas. Dites quand même comme ça à l'intuition, est-ce que vous pensez qu'il y a plus de chance qu'ils soient premiers ou qu'ils ne le soient pas ?
(Je vous laisse mariner mais je vous promets que je vous donnerai la réponse ... un jour :id: :we: :we: )
Proba pour que 2 nombres soient premier entre eux
11 messages
- Page 1 sur 1
Salut
je dis peut-être une bétise, mais rapidement, je pense que ça se fait avec une disjonction des cas sur les congruences des nombres modulo 2, 3, 4 etc..
Et donc finalement je dirais que ça fait la somme des inverses des carrés d'entiers, de mémoire pi^2/6.
edit : euh non en fait c'est plus probable 6/pi^2, tant qu'à faire, autant que ce soit inférieur à 1 ^^
Mais là je vois plus pourquoi...
je dis peut-être une bétise, mais rapidement, je pense que ça se fait avec une disjonction des cas sur les congruences des nombres modulo 2, 3, 4 etc..
Et donc finalement je dirais que ça fait la somme des inverses des carrés d'entiers, de mémoire pi^2/6.
edit : euh non en fait c'est plus probable 6/pi^2, tant qu'à faire, autant que ce soit inférieur à 1 ^^
Mais là je vois plus pourquoi...
Bon je vous ai promis la démonstration :
Il y a 4 cas possible pour a et b, soient ils sont tous les deux pairs, soit ils sont impairs soit il y en a un de pair et l'autre impair. La probabilité qu'ils soient tous les deux pars est 1/4 donc celle qu'il ne soient pas tous les deux pairs est 3/4.
De même la probabilité pour qu'ils ne soient pas tous les deux divisibles par 3 vaut 8/9.
Celle pour qu'ils ne soient pas tous les deux divisibles par un nombre p premier vaut 1 -1/p^2 , (en effet, il y a p restes par p possibles pour a comme pour b donc p^2 couples de restes possibles et seul un de ces p^2 couples correspond à la divisibilité de a et b par p).
Toutes ces probabilités étant indépendantes, elles sont multiplicatives. La probabilité pour que a et b soient premiers entre eux peut donc s'écrire q = (3/4).(8/9).(24/25) .... etc que l'on peut noter Produit (1- (1/p^2)) pour tous les p premiers (On appelle produit Eulerien un produit infini indexé sur les les nombres premiers).
Bon jusqu'ici c'était pas trop compliqué. Maintenant on va voir un truc beaucoup plus étonnant puisque ça fait comprendre le lien entre la fonction dzeta et les nombres premiers.
La fonction dzeta c'est la somme de l'inverse des nombre à la puissance s
1+ (1/2^s)+(1/3^s)+ ......
Mais d'abord si on calcule 1+(1/p^s)+(1/p^2s)+(1/p^3s)+ ... on trouve une somme de suite géométrique et ça vaut 1/(1-(1/p)^s)
Imaginez que l'on reprenne notre produit infini de tout à l'heure
Produit (1- (1/p^2)) en remplaçant chaque terme par 1+(1/p^2)+(1/p^4)+(1/p^6)+ ... , Quand on va faire le produit terme à terme on va forcement reconstituer tous les entiers et retomber sur la suite infini dzeta (2)
Et donc 1/q= 1+1/2^2+1/3^2+ ....etc....
Reste à calculer cette somme qui traîne dans tous les manuels.
Personnellement j'adore la démonstration ancienne d'Euler (mais qui est considérée aujourd'hui comme un peu limite d'un point de vue rigueur).
Mais je ne résiste pas :
on part de sin(x)/x = 1-x^2/6+ ... développement de taylor du sin
Euler le considérait comme un polynôme infini et ne voyait pas pourquoi il ne pourrait pas se factoriser comme tout bon polynôme en (1-x/a)(1-x/b) ... à condition que l'on connaisse ses zéros. Mais justement on les connaît les zéros puisque ce sont les valeurs qui annulent le sin soit + ou - pi, 2.pi, etc...
Donc le polynôme s'écrit (en regroupant les zéro + pi et - pi)
(1-x^2/pi^2)(1-x^2/(2.pi)^2) ......(1-x^2/(n.pi)^2+ ....
qui est donc égal aussi à 1-x^2/6+ ...
Pour fabriquer le terme en x^2 donc -1/6, on doit prendre des 1 dans tous les produits et un 1/(n.pi)^2 et donc 1/6 = 1/pi^2+....+1//(n.pi)^2+...
en chassant le pi^2 on trouve donc bien que pi^2/6 est la somme des inverses des carrés des nombres.
C'est fini, 1/q = pi^2/6
et donc la probabilité pour que 2 nombres tirés au hasard soient premier entre eux est de 6/pi^2 soit environ 0,608
Il y a plus de chances que deux nombres soient premiers entre eux plutôt qu'ils ne le soient pas.
Voilà comment un résultat de théorie des nombres parlant de nombres premiers fait intervenir Pi. Moi personnellement je trouve ça assez super.
Il y a 4 cas possible pour a et b, soient ils sont tous les deux pairs, soit ils sont impairs soit il y en a un de pair et l'autre impair. La probabilité qu'ils soient tous les deux pars est 1/4 donc celle qu'il ne soient pas tous les deux pairs est 3/4.
De même la probabilité pour qu'ils ne soient pas tous les deux divisibles par 3 vaut 8/9.
Celle pour qu'ils ne soient pas tous les deux divisibles par un nombre p premier vaut 1 -1/p^2 , (en effet, il y a p restes par p possibles pour a comme pour b donc p^2 couples de restes possibles et seul un de ces p^2 couples correspond à la divisibilité de a et b par p).
Toutes ces probabilités étant indépendantes, elles sont multiplicatives. La probabilité pour que a et b soient premiers entre eux peut donc s'écrire q = (3/4).(8/9).(24/25) .... etc que l'on peut noter Produit (1- (1/p^2)) pour tous les p premiers (On appelle produit Eulerien un produit infini indexé sur les les nombres premiers).
Bon jusqu'ici c'était pas trop compliqué. Maintenant on va voir un truc beaucoup plus étonnant puisque ça fait comprendre le lien entre la fonction dzeta et les nombres premiers.
La fonction dzeta c'est la somme de l'inverse des nombre à la puissance s
1+ (1/2^s)+(1/3^s)+ ......
Mais d'abord si on calcule 1+(1/p^s)+(1/p^2s)+(1/p^3s)+ ... on trouve une somme de suite géométrique et ça vaut 1/(1-(1/p)^s)
Imaginez que l'on reprenne notre produit infini de tout à l'heure
Produit (1- (1/p^2)) en remplaçant chaque terme par 1+(1/p^2)+(1/p^4)+(1/p^6)+ ... , Quand on va faire le produit terme à terme on va forcement reconstituer tous les entiers et retomber sur la suite infini dzeta (2)
Et donc 1/q= 1+1/2^2+1/3^2+ ....etc....
Reste à calculer cette somme qui traîne dans tous les manuels.
Personnellement j'adore la démonstration ancienne d'Euler (mais qui est considérée aujourd'hui comme un peu limite d'un point de vue rigueur).
Mais je ne résiste pas :
on part de sin(x)/x = 1-x^2/6+ ... développement de taylor du sin
Euler le considérait comme un polynôme infini et ne voyait pas pourquoi il ne pourrait pas se factoriser comme tout bon polynôme en (1-x/a)(1-x/b) ... à condition que l'on connaisse ses zéros. Mais justement on les connaît les zéros puisque ce sont les valeurs qui annulent le sin soit + ou - pi, 2.pi, etc...
Donc le polynôme s'écrit (en regroupant les zéro + pi et - pi)
(1-x^2/pi^2)(1-x^2/(2.pi)^2) ......(1-x^2/(n.pi)^2+ ....
qui est donc égal aussi à 1-x^2/6+ ...
Pour fabriquer le terme en x^2 donc -1/6, on doit prendre des 1 dans tous les produits et un 1/(n.pi)^2 et donc 1/6 = 1/pi^2+....+1//(n.pi)^2+...
en chassant le pi^2 on trouve donc bien que pi^2/6 est la somme des inverses des carrés des nombres.
C'est fini, 1/q = pi^2/6
et donc la probabilité pour que 2 nombres tirés au hasard soient premier entre eux est de 6/pi^2 soit environ 0,608
Il y a plus de chances que deux nombres soient premiers entre eux plutôt qu'ils ne le soient pas.
Voilà comment un résultat de théorie des nombres parlant de nombres premiers fait intervenir Pi. Moi personnellement je trouve ça assez super.
ca marche,mais tout ceci reste tres heuristique(je ne parle pas du calcul de zeta(2 ) que tu a toi meme admis heuristique).Comme il a été dit plus haut,on ne peut vraiment parler de probabilités,on peut seulement définir une pseudo probabilité comme limite de probas uniformes sur [0,n].Malheureusement,cette pseudo proba n a pas autant de propriétés qu une proba normale,et n est par exemple pas sigma-additive,ce qui entraine certains problemes d interversions de limites.Pour etre precis,voila le passage de ta demo qui demande justification:si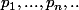 la suite des premiers nombres premiers,je suis d accord que l on peut montrer facilement que pour tout n,la "probabilité" que a et b ne sont divisible par aucun des
la suite des premiers nombres premiers,je suis d accord que l on peut montrer facilement que pour tout n,la "probabilité" que a et b ne sont divisible par aucun des 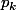 pour
pour 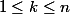 est
est ) .Mais comment en deduis tu que la probabilité que a et b ne soient divisibles par aucun nombre premier vaut
.Mais comment en deduis tu que la probabilité que a et b ne soient divisibles par aucun nombre premier vaut 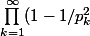) .Il faut justifier une interversion de limite qui n a a priori rien d évidente..
.Il faut justifier une interversion de limite qui n a a priori rien d évidente..
pourquoi tu dis "interversion de limite" ? je comprend que le passage à l'infini peut poser problème (c'est comme les espaces vectoriels de dim infini, c'est jamais simple) mais si le produit converge, on devrait pouvoir montrer qu'à ce moment là, la solution est valide.
C'est quoi des pseudo probabilités ? pourquoi tu dis qu'elles ne sont pas sigma additives ?
C'est quoi des pseudo probabilités ? pourquoi tu dis qu'elles ne sont pas sigma additives ?
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
