Polynômes...
14 messages
- Page 1 sur 1
Polynômes...
Bonsoir,
Je cherche à répondre à cette question...
trouver tous les polynômes tels que p(0)=p'(1)=1 , p(1)=p'(0)=0
Un indice please?
Je cherche à répondre à cette question...
trouver tous les polynômes tels que p(0)=p'(1)=1 , p(1)=p'(0)=0
Un indice please?
Re: Polynômes...
Bonsoir,
Ça peut se traduire en un système de congruences, et le théorème chinois entre en action.
Ça peut se traduire en un système de congruences, et le théorème chinois entre en action.
Re: Polynômes...
J'ai trouvé un polynôme qui convient P0(X)=3/2 X^4-5/2X^2+1.
Pui j'ai montré que P vérifie les conditions souhaitées si et seulement si P est de la forme P0+X^2(X−1)^2R avec R∈R[X].
Vos avis?
Pui j'ai montré que P vérifie les conditions souhaitées si et seulement si P est de la forme P0+X^2(X−1)^2R avec R∈R[X].
Vos avis?
Re: Polynômes...
Bonjour,
le polynôme que vous avez trouver est un des polynômes qui vérifient les conditions demandées. Mais la question est "tous les polynômes".
un polynôme c'est :
=\sum_{i=0}^{i=n} a_i x^i)
=\sum_{i=0}^{i=n} ia_i x^{i-1})
en appliquant les conditions p(0)=p'(1)=1 , p(1)=p'(0)=0, vous trouvez une condition sur les ( qui est vérifiée par le polynôme que vous avez trouvé)
( qui est vérifiée par le polynôme que vous avez trouvé)
le polynôme que vous avez trouver est un des polynômes qui vérifient les conditions demandées. Mais la question est "tous les polynômes".
un polynôme c'est :
en appliquant les conditions p(0)=p'(1)=1 , p(1)=p'(0)=0, vous trouvez une condition sur les
Re: Polynômes...
Ton polynôme P0 ne convient pas. Sa dérivée en 0 n'est pas nulle.
J'explique le système de congruences :
Les conditions en 0 peuvent se traduire par le fait que est congru à
est congru à  modulo
modulo  , et les conditions en 1 par le fait que
, et les conditions en 1 par le fait que  est congru à
est congru à 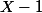 modulo
modulo ^2) .
.
Le théorème des restes chinois, avec l'égalité de Bezout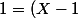^2(2X+1)-X^2(2X-3)) nous dit que les solutions sont les polynômes
nous dit que les solutions sont les polynômes  congrus à un certain polynôme que je te laisse calculer modulo
congrus à un certain polynôme que je te laisse calculer modulo ^2) .
.
Ce sont des calculs un peu lourds. Il est moins fatigant de chercher l'unique polynôme de degré 3 satisfaisant les conditions (les autres lui sont congrus modulo^2) . Les conditions en 0 imposent au polynôme d'être de la forme
. Les conditions en 0 imposent au polynôme d'être de la forme 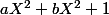 et les conditions en 1 permettent de déterminer
et les conditions en 1 permettent de déterminer  et
et  .
.
On peut aussi signaler la méthode d'interpolation de Hermite par les différences divisées :
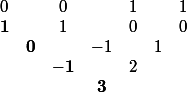
qui donne\times X^2 + \mathbf{3}\times X^2(X-1)) .
.
J'explique le système de congruences :
Les conditions en 0 peuvent se traduire par le fait que
Le théorème des restes chinois, avec l'égalité de Bezout
Ce sont des calculs un peu lourds. Il est moins fatigant de chercher l'unique polynôme de degré 3 satisfaisant les conditions (les autres lui sont congrus modulo
On peut aussi signaler la méthode d'interpolation de Hermite par les différences divisées :
qui donne
Re: Polynômes...
Tu as raison, ton polynôme convient, je l'avais mal lu.
Comment l'as-tu trouvé ?
Ci-dessus, j'ai donné trois moyens de procéder. Aucun ne donne ton polynôme (qui est bien sûr congru aux autres modulo^2) ).
).
Comment l'as-tu trouvé ?
Ci-dessus, j'ai donné trois moyens de procéder. Aucun ne donne ton polynôme (qui est bien sûr congru aux autres modulo
Re: Polynômes...
En traçant une courbe qui admet une tangent horizontale en (0;1) et y=x-1 en (1;0) .
Une fct paire du 4ème degré vérifie ces deux conditions...
Mais une cubique peut convenir aussi...
Une fct paire du 4ème degré vérifie ces deux conditions...
Mais une cubique peut convenir aussi...
Re: Polynômes...
Exact. Pour la cubique avec une même méthode j'ai trouvé P0(x)=3x^3-4x^2+2.
En conclusion du problème, il y a une infinité de solutions de la forme P(x)=P0(x)+x^2(x-1)^2Q(x) avec Q un polynôme Quelconque.
En conclusion du problème, il y a une infinité de solutions de la forme P(x)=P0(x)+x^2(x-1)^2Q(x) avec Q un polynôme Quelconque.
Re: Polynômes...
Oui, c'est cela, c'est le polynôme que j'ai indiqué comme résultat de la méthode des différences divisées. Il y a unicité pour le degré  .
.
Re: Polynômes...
euler13190 a écrit:Exact. Pour la cubique avec une même méthode j'ai trouvé P0(x)=3x^3-4x^2+2.
tu es sûr ?
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
