Un point dans le Vide... spatial...

[PzKd]

Bonjour à tous,

Je suis en pleine réflexion sur un sujet lié à la géométrie dans l'Espace (oui, oui, avec un E, Les étoiles, les planètes, tout ça).

En ce moment, je joue beaucoup (trop) à un jeu ayant pour thème l'exploration spatiale. Et j'en suis venu à me poser la question : où suis-je réellement et comment être sûr que je suis au bon endroit ?

Grâce au calculateur de bord de mon vaisseau, je peut connaitre la distance (mais pas la direction, ni le sens) qui me sépare de n'importe quel étoile dont je connais le nom.

Ma question est : de combien de points de référence vais-je avoir besoin pour savoir précisément où je suis dans le Vide ?

Un grand merci d'avance à ceux qui vont pouvoir m'aider.

[nodjim]

Tu as besoin de 4 pts de référence non coplanaires, je dirais.

[lulu math discovering]

oui c'est ça

D'ailleurs, si tu t'intéresse à l'observation, sache que beaucoup de télescopes ont un système de guidage automatique.

Mais pour qu'il marche, il faut qu'il connaisse sa position. Du coup on pointe 3 étoiles considérées comme point fixe pour se repérer.

Sur Terre, on n'a pas besoin d'un 4ème étoile parce qu'on veut trouver un autre objet de la voute céleste qui est considérée comme une demi-sphère, soit un plan.

[PzKd]

J'aimerais beaucoup me lancer dans l'observation astronomique mais j'habite dans un endroit à fort pollution lumineuse (le ciel de Paris est "orange" en permanence). Alors du coup, je me rattrape sur un jeu vidéo (qui par ailleurs simule de manière plutôt réaliste ce qu'est notre galaxie) ^^

Maintenant que j'ai ma réponse, j'aimerais pouvoir poser une autre question :

J'ai visité une étoile E1, et j'ai noté les 4 distances de référence D1, D2, D3 et D4, respectivement la distance entre E1 et Sol, E1 et Sag A*, E1 et Aldebaran, E1 et Betelgeuse.

Maintenant je visite une étoile E2 et je note les 4 distances de référence D1', D2', D3' et D4'.

Existe t-il une formule me permettant de connaitre la distance entre E1 et E2 ?

[nodjim]

3 pts ne suffisent pas. N'oublie pas qu'on ne connait pas le lieu des pts de référence, mais seulement leur distance. Or il existe 2 pts d'observation qui sont à égale distance de 3 pts de référence (symétrie par rapport au triangle formé par les 3 pts). Il en faut donc un 4ème pour lever l'ambiguïté.

[lulu math discovering]

Il ne faut pas les distances, il faut tes coordonnées par rapport à ces étoiles, si on les considère fixes.
Dans un plan, il faut trois points pour faire un repère (A;B;C), et il en faut 4 en 3D.

[PzKd]

Il ne faut pas les distances, il faut tes coordonnées par rapport à ces étoiles, si on les considère fixes.
Dans un plan, il faut trois points pour faire un repère (A;B;C), et il en faut 4 en 3D.

Le problème, c'est que je n'ai pas les coordonnées des points. Je n'ai que les distances.

[lulu math discovering]

Dans ce cas, il faut que, pour chaque étoile, tu te place à 4 endroits de l'espace (non alignés) pour repérer chaque étoile.
Ensuite seulement tu pourras introduire des coordonnées.

[PzKd]

J'ai bien peur ne pas avoir compris. Le jeu ne me donne pas les coordonnées. Seulement les distances entre ma position et les étoiles environnantes.

[lulu math discovering]

Dans ce cas, il faut que, pour chaque étoile, tu te place à 4 endroits de l'espace (non alignés) pour repérer chaque étoile.

Tu auras ainsi 4 distances à chaque étoile. Ce qui te permettra de la repérer.

[Robot]

Je suppose que tu connais aussi les distances entre les étoiles de référence ?
En écrivant que le déterminant de Cayley-Menger construit sur les deux étoiles visitées E1 et E2 et trois des étoiles de références est nul, on obtient une équation du second degré dont une des racines est le carré de la distance entre E1 et E2. On peut choisir entre les deux racines en utilisant la quatrième étoile de référence.

[PzKd]

Tu auras ainsi 4 distances à chaque étoile. Ce qui te permettra de la repérer.

Je ne cherche pas à la repérer (depuis la Terre) mais à calculer sa distance entre mon point actuel, E1, (mon vaisseau se trouve quelque part dans le bras Écu-Croix) et une autre étoile E2. Le tout en utilisant les distances de références.

Je suppose que tu connais aussi les distances entre les étoiles de référence ?

Tu veux dire, par exemple, la distance entre D1 et D2 ? Oui, je connais cette distance.

JEn écrivant que le déterminant de Cayley-Menger construit sur les deux étoiles visitées E1 et E2 et trois des étoiles de références est nul, on obtient une équation du second degré dont une des racines est le carré de la distance entre E1 et E2. On peut choisir entre les deux racines en utilisant la quatrième étoile de référence.

Alors, j'ai cherché un peu ce qu'était le "déterminant de Cayley-Menger" et j'ai trouvé ça :
http://dpt-info.u-strasbg.fr/~mathis/Enseignement/CG/Cours/5Cayley-Menger.pdf

C'est en anglais mais je pense avoir compris le principe. Grosso modo on va construire un "truc" composé de six points (E1, E2, D1, D2, D3 et D4) avec des contraintes de distance. Et l'aide d'une matrice on va pouvoir déterminer la distance inconnue (à savoir E1-E2). J'ai bon ?

[Robot]

En très gros oui, mais il faut régler les détails.
Ce que je suggère :
Soit d le carré de la distance inconnue (entre E1 et E2).
L'annulation du déterminant de Cayley-Menger sur E1,E2,D1,D2,D3 donne une équation du second degré en d.
L'annulation du déterminant de Cayley-Menger sur E1,E2,D1,D2,D4 donne une autre équation du second degré en d.
L'élimination de d^2 entre ces deux équations donne une équation du premier degré en d qu'on résoud facilement.

[PzKd]

En très gros oui, mais il faut régler les détails.
Ce que je suggère :
Soit d le carré de la distance inconnue (entre E1 et E2).
L'annulation du déterminant de Cayley-Menger sur E1,E2,D1,D2,D3 donne une équation du second degré en d.
L'annulation du déterminant de Cayley-Menger sur E1,E2,D1,D2,D4 donne une autre équation du second degré en d.
L'élimination de d^2 entre ces deux équations donne une équation du premier degré en d qu'on résoud facilement.

Je m'en vais récolter quelques données numériques et je reviens vers toi, quand je commencerais à remplir la matrice ^^

[nodjim]

Je ne suis p

[PzKd]

Après, je sèche, aucune idée comment je peut obtenir mes équations.

[Robot]

Il semble que tu aies mal lu la définition des déterminants de Cayley-Menger.
1°) Il s'agit de déterminants. Sais-tu bien ce qu'est un déterminant ? Tu les écris comme des matrices (avec des crochets ouvrants et fermants). Ecrire qu'un déterminant est nul, c'est directement une équation.
2°) Ce qui figure dans le déterminant de Cayley-Menger, c'est les carrés des distances entre les points, et pas les distances comme tu l'écris.

[PzKd]

Il semble que tu aies mal lu la définition des déterminants de Cayley-Menger.

Pour le coup, j'applique de façon bête et méchante ce qui est écrit dans le pdf dont j'ai donné le lien.

1°) Il s'agit de déterminants. Sais-tu bien ce qu'est un déterminant ? Tu les écris comme des matrices (avec des crochets ouvrants et fermants). Ecrire qu'un déterminant est nul, c'est directement une équation.

J'ai déjà entendu le terme "déterminant" dans la même phrase que le mot "matrice" mais ça s'arrête là. C'est triste à dire, mais mon niveau en math est celui d'un élève de seconde générale.

2°) Ce qui figure dans le déterminant de Cayley-Menger, c'est les carrés des distances entre les points, et pas les distances comme tu l'écris.

Là encore, j'ai appliqué ce que j'ai lu dans le pdf. Je n'ai vu nulle part que les distances étaient au carré.

[Robot]

J'ai déjà entendu le terme "déterminant" dans la même phrase que le mot "matrice" mais ça s'arrête là. C'est triste à dire, mais mon niveau en math est celui d'un élève de seconde générale.

Bon, ben je crois qu'il vaut mieux arrêter là alors. Pour les déterminants de Cayley-Menger, la marche est trop haute. Tu peux à la rigueur les utiliser comme boîte noire avec un logiciel de calcul formel.

Là encore, j'ai appliqué ce que j'ai lu dans le pdf. Je n'ai vu nulle part que les distances étaient au carré.

Là tu pousses un peu ! Transparent 4 de la présentation, je cite : where

[alphamethyste]

ne t'inquiète pas c'est simple (je t'explique en cinq étapes)

1. definition generale(comprendre pourquoi on parle du determinant de Cayley

le determinant d'une matrice carrée M parfois se note Det(M) est un nombre réel (en general)
ici pour ce qui t'occupe (la guerre des etoiles) le determinant est un nombre réel

on se place dans l'espace physique (dit aussi affine et euclidien de dimension 3)

-si tu as trois points A,B,C distinctsmais que tu ne connais pas leurs coordonnées mais uniquement leur distances entre eux . notation d(x,y) est la distance entre x et y

alors le determinant de Cayley-Mender te permet de savoir si tes trois points sont alignés

pour le savoir il te faut verifier

Det

-si tu as quatre points A,B,C,D distinctsmais que tu ne connais pas leurs coordonnées mais uniquement leur distances entre eux .

alors le determinant de Cayley-Mender te permet de savoir si tes quatres points sont coplanaires

pour le savoir il te faut verifier

Det


2.notation des coefficients d'une matrice
une nxp matrice est une matrice de n lignes et p colonnes composantes (et dite carrée si n=p et on dit alors que n est l'ordre de cette matrice carré)
la premiere ligne est celle située tout en haut
la premiere colonne est celle située tout à gauche

par exemple en notant M une matrice alors la composante notée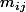
est située à la i ième ligne et à la j ieme colonne

3.le symbole d'anti symetrie

on note est le coefficient anti symetrique

ce symbole peut prendre la valeur 0 ou 1 ou -1

et i,j,k,l sont des entiers naturels non nuls

on dit que lorsque tes indices i,j,k,l sont dans l'ordre
alors ce ordre est dit naturel

alors

lorsque deux quelconques au moins des indices sont identiques

par exemple car le premier et le troisieme indice sont identiques

lorsque l'ordre des indices proviens d'un nombre pair de permutations à partir de l'ordre naturel

par exemple parce que 1234 -> 2134 -> 2143 deux permutations

lorsque l'ordre des indices proviens d'un nombre impair de permutations à partir de l'ordre naturel

par exemple parce que 1234 -> 2134 une permutation

4.Convention de sommation d'Einstein

ici il s'agit d'un exemple (attention c'est un exemple parmis d'autre car au chapitre suivant c'est un autre exemple) appliqué pour determiner un composante situé à la ligne i et à la colonne j d'une matrice C et qui est le produit de deux matrices A et B

tu dispose de composantes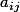 d'une nxp matrice A
et que tu dispose de composantes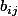 d'une pxm matrice B

alors le produit AB=C est une nxm matrice de composantes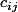

tu obtiens

tu note tout simplement et on comprend qu'il s'agit d'une sommation d'Einstein

5.calcul du determinant d'une matrice carrée

soit M une matrice carrée d'ordre 3 de composantes notées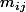

alors le determinant de M est donné par la convention de sommation d'Einstein suivante

Det
donc sommation avec i,j,k prennant les valeur de 1 à 3