Bonjour, voila je m’ennuyais et après quelques petites observations bien sur

j'en suis arrivé a me poser cette conjecture :
La somme de l'ensemble des solution complexe d'une racines

-ième de

est nulle pour tout

entier naturel non 0 ou 1.
Ou en une seule formule :
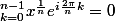
Pour
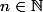
\ {0;1} et
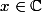
J'aimerais savoir si il y a des gens ici qui pourraient m'aider ou avoir une idée de comment démontrer vrai cette conjecture (ou bien le démontrer faux

)
Donc parce que je pense que vous n'allez pas vraiment comprendre ce que j'ai dis plus haut (Parce que c'est pas clair ou bien que je me suis mal exprimé vu que j'ai tenter de le rendre le plus compacte possible mais que j'ai peut-être du coup utiliser de mauvaises notions) je vais tenter de vous expliquer cette conjecture.
Tout d'abord, qu'est-ce que j'entend par solutions d'une racine
n-ième de
x ce sont tout les nombres complexes qui répondent a l'équation
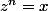
. Ce que ma conjecture dit c'est que la somme (d'où la notation sigma) de ces nombres

est nulle où

= 2;3;4... Le

ici est une nombre quelconque qui n'a surement pas d’importance (il faut peut-être que
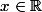
mais c'est pas sûr, mais je vais pas vous le cacher, j'ai un peu la flemme de voir pour

)
Le bidule
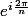
est une formule qui permet d'avoir une des solutions et le petit

permet d'obtenir tout les résultat en tant qu'index (même si ici mon explication n'est pas claire et que je ne le démontre pas pour des raisons de facilité croyez-moi, ca marche)
Mon théorème considère toutes les valeurs de
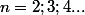
. En effet, je ne peut pas considérer
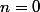
car
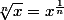
donc si
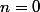
on aurais une situation de
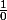
ce qui serait... problématique et j'ai omis

car ça donnerais

(donc le même nombre) en sortie (du moins sur les quelques valeurs que j'ai tester mais de toute façon ça ne donne pas 0)
J'ai par ailleurs tester ma conjecture avec wolfram alpha (testez la vous aussi avec cet input :
- Code: Tout sélectionner
sigma from t=0 to n-1 of 2^(1/(n))*e^(i*2*pi*t*(1/(n)))

). Il donne bien 0 pour tout

entier supérieur à 2 mais pour certaines valeurs (pour

impair), il output des fois un charabia plein de racine et autres nombres irrationnels mais si on clique dessus (on cherche donc à savoir ce qu'ils valent) ils donnent bien 0

.
J'ai déjà une piste pour tout

pair qui consisterais à dire que car c'est une racine

-ième où

est pair, les solutions ont une symétrie vis à vis de l'axe des abysses et donc tous ont un nombre qui a pour partie complexe son opposé mais aussi une symétrie vis à vis de l'axe des ordonnés et ont donc chacun un nombre qui a pour partie réelle opposé (du moins ça tient la route jusqu'à la puissance 4ème)

. Après je sais pas. Peut-être en utilisant les vecteurs.
Voila j'espère avoir été assez clair ici, n’hésitez pas a me demander de vous expliquer si vous n'avez pas compris certaines choses et j'espère que vous aurez des piste pour m'aider

.
edit: Toujours utile de préciser quand même :

ici est l'unité imaginaire

 ). Il donne bien 0 pour tout
). Il donne bien 0 pour tout 