Petit probleme trygo

[Tahitipierre]

Messieurs dame bonjour!
voici un petit schéma qui représente un spot d'éclairage (J) qui doit éclairé un objet (bd)
Je connais [ab], [bd] et l'angle BJD
je doit déterminé [aj]
y a t'il la possibilité d'établir une formule d’après ces donnés. Le but serais de mettre cette formule sur un tableur EXEL.



au cas ou l'image ne s'affiche pas voici un lien https://www.dropbox.com/s/dqo61qcz9qjq9h9/faisseau%20eclairage%20.jpg

Merci pour votre lecture.

[WillyCagnes]

ia Orana tane,

soit
jb² = bd² +jd² -2(bd)(jd)cos(bdj)

or
ja² +ad²=jd² (triangle rectangle en A)
et
ja² +ab²= jb²

jb² = bd² +( ja² +ad²) -2(bd ) racine(ja²+ad²) cos(bdj)

ja²+ab² =bd² +( ja² +ad²) -2(bd ) racine(ja²+ad²) cos(bdj)

ab² = bd² +ad² -2(bd)racine(ja²+ad²) cos(bdj)

(ab² -bd² -ad²)/(-2(bd)cos(bdj)] = racine(ja²+ad²)

on élève au carré

[(ab² -bd² -ad²)/(-2(bd)cos(bdj))]² = ja² -ad²

ja²=[(ab² -bd² -ad²)/(-2(bd)cos(bdj))]² +ad²

ensuite ja =racine carré de l'expression


aie! je me suis trompé d'angle (bdj) inconnu
essaie de le refaire en partant de

bd² = jb² +jd² - 2(jb)(jd)cos(bjd)

[Ben314]

Salut,

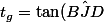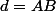
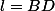
Si on pose ) ; ; (tous connus)

Alors tu veut que et que
Or

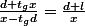
Donc l'équation à résoudre est , c'est à dire qui est du second degré...