Bonjour.
J'ai vu que la Corée du Nord avait été disqualifiée des OIM à deux reprises, en 1994, et en 2010, et je me demandais comment c'était possible.
Olympiades Internationales de Mathmatiques.
8 messages
- Page 1 sur 1
Voilà j'ai retrouvé ma source : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=643&t=357005
Bonne lecture
Bonne lecture
Pour ceux qui ont la flemme de lire :
Voici l'exercice en question :
Le lemme que 4 participants sur 6 ont utilisé de la même manière :
 - g\left(b\right) \right. \Rightarrow p \left| a-b \right.) pour tout
pour tout 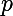 premier .
premier .
Officially, there were very strong correspondences in the solutions of the participants. Thus the majority began Problem 3 with the same lemma and use in another problem a clever notation which none of the participants, but only the proposed solution, had shown. And also a little more. Totally, due to these "striking circumstances", the disqualification was put to a vote, and with one vote against (North Korea), many abstaining and predominantly yes-votes, the disqualification decided.
Voici l'exercice en question :
Trouver toutes les fonctionstelles que
soit un carré parfait pour tout
de
.
Le lemme que 4 participants sur 6 ont utilisé de la même manière :
De loin, ça a l'air injuste comme décision..Tout ceci basé sur le fait que pour un seul exercice, et un seul argument de cet exercice, 4 gars sur les 6 ont fait la même chose. Je veux pas dire, mais c'est comme pour les anniversaires, y avait des chances qu'un tel truc se passe quelque part.. Surtout quand les candidats sont bons et qu'il n'y a pas tellement de solutions différentes possibles pour résoudre le problème
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
