bonjour à tous ;
s'il vous plais j'ai une question que je n'arrive pas a la résoudre dans un DM:
z^3 -3iz +1-i=0 et on a uv=i et u+v=z
la question est :
montrer que si z sont les solutions de l’équation précédente alors nécessairement u^3 et v^3 sont les solutions de l’équation : w^2 +(1-i)w-i=0 .
Mrthode de cardon
3 messages
- Page 1 sur 1
Re: mrthode de cardon
Bonjour,
Petite faute de frappe, il s'agit plutôt de la méthode de Cardan, qui permet de trouver les racines des polynomes de degré 3. Je pense qu'une petite recherche Google te permettra de trouver réponse à ta question, car cette méthode est développée sur pas mal de sites.
Petite faute de frappe, il s'agit plutôt de la méthode de Cardan, qui permet de trouver les racines des polynomes de degré 3. Je pense qu'une petite recherche Google te permettra de trouver réponse à ta question, car cette méthode est développée sur pas mal de sites.
Re: mrthode de cardon
Bonjour,
Plutôt que de chercher sur internet, on peut aussi se prendre par la main pour faire ce qui est attendu :
On suppose que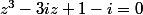 . (*)
. (*)
On suppose aussi que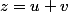 avec
avec 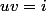 .
.
On remplace par u+v dans (*), et on simplifie en utilisant
par u+v dans (*), et on simplifie en utilisant 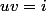 .
.
Enfin, on se rappelle que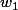 et
et 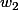 sont les solutions de
sont les solutions de 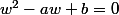 si et seulement si
si et seulement si 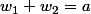 et
et 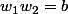 .
.
Plutôt que de chercher sur internet, on peut aussi se prendre par la main pour faire ce qui est attendu :
On suppose que
On suppose aussi que
On remplace
Enfin, on se rappelle que
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
