Montrer qu'un nombre est irrationnel

[sml99]

Bonjour a tous , j'espère que vous m'aidez pour montré que
"2-3*racine(2) " est irrationnel .
Merci .

[Ben314]

Salut,
Vu que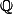 est un corps, ton réel est rationnel si et seulement si l'est.
Or on sait bien que ce n'est pas le cas.

S'il y en a que ça intéresse, je viens de lire il y a peu une preuve légèrement différente de la preuve usuelle pour montrer que, si est un entier naturel non carré (d'un entier) alors 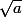est irrationnel :

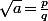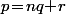On part d'un entier quelconque , on suppose que (irréductible) et considère la division euclidienne de par : avec .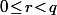
Si était non nul on aurait ce qui est absurde vu 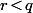et 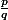irréductible.
Donc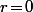 et 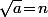est entier : est donc le carré d'un entier.

[Pseuda]

Bonsoir,

@Ben314, pas mal.

@sml99
Peut-être que Ben314 a été un peu elliptique. Raisonne par l'absurde : si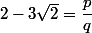 alors 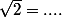un nombre rationnel, ce qui est faux.