Mon infini est plus grand que le tiens !

[Elerinna]

euh ? ... Je vais p't'être prendre la cafetiére tout compte fait ?
Je vois pô bien la bijection entre N et Z là !?
Avec n entier naturel f(n)=n/2 ... je vois pô bien où il faut aller là. Peut'être le n=q/2 doit vouloir dire quelques chose ? Mais quoi ?
Si n est impair n/2 n'est plus un entier ... :hein2: ...

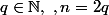
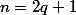
La notation signifie que n est pair. Si est impair, reste à établir.. :id:

Ce qu'il est important de retenir, c'est qu'on n'a pas besoin d'exhiber une bijection entre 2 ensembles pour montrer qu'ils ont le même nombre d'éléments, il suffit d'avoir 2 injections ou 2 surjections. Le théorème de Cantor-Bernstein nous assure alors qu'il y a une bijection entre les 2 ensembles et donc qu'ils ont le même cardinal.

La culture théorique de fond apporte de l'assise aux gens scolaires sans résoudre toutes les astuces.
Or je maintiens qu'une simple bijection mise en exergue est une condition suffisante de l'équipotence.
Le fait d'en déterminer (au moins) une entre les différents ensembles sus-cités n'est qu'une formalité.

[Elerinna]

Ah ok Elirenna. Mais tu te serais pô trompé alors en mettant :

Car là c'est n qui est un entier, on n'a pô encore défini q ?!
Donc je crois que le truc c'est de faire un peu comme j'ai fait nan ?! C'est à dire les nombres pairs vont parcourir tout les nombres entiers positifs, et les impairs aurront pour mission de parcourir tout les entiers négatifs !?
Ça donnerai un truc comme ça :
?

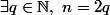
Si est pair alors : la définition de va de soi par abus mais elle doit s'expliciter.

Bravo pour le constat des entiers impairs à un constat minime près: 0 est ainsi atteint 2 fois (enlève -1) !

[Elerinna]

Ah bah vi !
Donc ça ferait :

C'est bien ça ?
Pour la définition de n et q je ne suis pô certain de ce qui importe le plus à définir. En faite je connais pô trop les conventions d'écritures ...

Le problème subsistera: retranche le 1 dans pour impair ce qui donne :

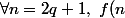[Judoboy]

@ Oktave : c'est exactement ce que tu as dessiné dans le dernier cas. Par contre fais attention avec tes schémas, tu peux pas dessiner aussi simplement quand on passe à des ensembles infinis.

Sinon t'as essayé de comparer N et N² ? (N² c'est l'ensemble des couples (p,n) pour p et n décrivant N)

[Elerinna]

(je réfléchi à clavier haut)
Quand n est impair il démarre à n=1 qui donnera (1-N)/2=0/2=0 ...
Ah tu veux dire faire (1-N)/2 -1 pour décaler le tout de -1 okokokok ...


EDIT :
J'ai vaguement réfléchi sans vraiment essayer Jud'
En faite en y réfléchissant je me suis demander comment on pouvait faire l'inverse. Prouver que l'un est définitivement plus grand que l'autre ?

Montre que tout élément de est identifiable comme borne d'un élément de s'il n'est pas dans alors

[Judoboy]

@ Oktave : en général c'est assez dur à prouver qu'un ensemble est "définitivement plus grand" qu'un autre, renseigne-toi sur l'argument diagonal de Cantor. On dit qu'un ensemble E est dénombrable lorsqu'il peut être mis en bijection avec N (soit card(E)=card(N))

En l'occurrence, N² n'est pas plus grand que N ; trouver une bijection ça peut se faire mais le plus simple est de donner une injection de N² dans N, vu qu'on a déjà une injection de N dans N². Indice: pense à l'unicité de la décomposition d'un nombre en facteurs premiers.

@ Elerinna : J'ai jamais dit qu'il y avait une topologie sous-jacente, pourquoi tu parles de limite ? Puis vous vous compliquez la vie pour rien, vu qu'exhiber une injection est bien plus simple.

i : x => 2*x si x est dans Z+
x=> (-2*x) -1 si x est dans Z-*

est une injection de Z dans N, et donc card(Z)<=card(N). L'injection inverse est triviale.

[Elerinna]

Sinon pour N et N² j'ai peut'être quelques chose mais je suis pô sur.
Grosso-merdo la même chose que ce l'on a fait, les entier pair sont divisé par deux pour refaire l'ensemble des entiers et les impairs sont augmenté de 1 pour être ensuite divisé par deux aussi.
Les pairs parcourent un ensemble des entiers naturels.
Et les impairs en parcourent un autre de plus.
C'est valide comme ça ?

Pense à des couples à lier pour la relation à établir entre ces deux ensembles ! Continue (:king: , :king2:)

@ Elerinna : J'ai jamais dit qu'il y avait une topologie sous-jacente, pourquoi tu parles de limite ? Puis vous vous compliquez la vie pour rien, vu qu'exhiber une injection est bien plus simple.

i : x => 2*x si x est dans Z+
x=> (-2*x) -1 si x est dans Z-*

est une injection de Z dans N, et donc card(Z)<=card(N). L'injection inverse est triviale.

Oui : tu ne fais grosso modo ici que donner une alternative à celle définie plus haut ("bornes" exclues).

[Judoboy]

Sinon pour N et N² j'ai peut'être quelques chose mais je suis pô sur.
Grosso-merdo la même chose que ce l'on a fait, les entier pair sont divisé par deux pour refaire l'ensemble des entiers et les impairs sont augmenté de 1 pour être ensuite divisé par deux aussi.
Les pairs parcourent un ensemble des entiers naturels.
Et les impairs en parcourent un autre de plus.
C'est valide comme ça ?

C'est une méthode, pas la plus simple. Réitère ton opération tu devrais voir la solution.

[Judoboy]

Maintenant imaginons que l'on ai une fonction à 1 millions de dÔllÂrs ! ..Ouais ! ..La célèbre fonction qui donne le Nième nombre premier. Disons qu'on la note P(n).
Alors si à chaque point (x;y) de N² on fait correspondre le nombre la décomposition en facteurs premiers étant unique chaque point renvoie à un entier unique.
C'est donc une injection de N² vers N.
Avec celle qui fait correspondre à chaque n (entier de N) le point (0;n) on a une injection dans l'autre sens. De N vers N² ... C'est !?
CQFD !?
J'ai bon ?! J'ai bon ?

Erf j'avais pas vu que t'avais répondu vu que t'avais juste édité tes messages sans en faire de nouveau, le thread n'était pas remonté...

En tout cas ça m'a l'air bon, tu as bien réussi à faire une injection de N² dans N ! (y avait quand même un peu plus simple, par exemple U(x,y) = 2^x*3^y, mais l'idée est à peu près la même) Et du coup il y a autant d'éléments dans N que dans N² (surprenant n'est-ce pas ?)


Maintenant que penses-tu du cardinal de Q ?

Edit : pour avoir les nombres pairs on prend 2*n, n appartenant à N. Pour avoir les nombres impairs on prend 2*n+1, n appartenant à N. C'est beaucoup plus simple et on ne rate pas 0 et 1.

[Judoboy]

Mais où s'arrétera l'empire des nombres entiers ?

Essaye avec R ou un intervalle de R pour voir

(indice : je t'invite à taper "argument diagonal" dans ton moteur de recherche)