Bonjour,
Attention, ceci n'est pas une question de cours!
Quelle conception du monde sous-tend la matrice, en mathématique?
Merci pour vos lumières.
La matrice
12 messages
- Page 1 sur 1
nordevan a écrit:Bonjour,
Attention, ceci n'est pas une question de cours!
Quelle conception du monde sous-tend la matrice, en mathématique?
Merci pour vos lumières.
elle présuppose la linearité et la dimension de taille finie, ce qui est vraie pour un tas de phenomenes (physique, chimique, biologique, etc....), mais qui est loin d'être une verité absolue. On sait depuis longtemps que la linéarité dans ce monde est l'exception et non pas la regle. La regle, c'est la non linearité et les fractales... Quant aux espaces de dimensions infinies, c'est pas ce qui manque...en somme, les matrices sont une vision partielle et etroite du monde, mais elles permettent de "nettoyer le terrrain", meme dans les cas les plus non lineaires, par l'étude locale des fonctions et autres "variétés centrales" ...
cesar a écrit:elle présuppose la linearité et la dimension de taille finie, ce qui est vraie pour un tas de phenomenes (physique, chimique, biologique, etc....), mais qui est loin d'être une verité absolue.
Bonjour,
je suis un peu étonné de cette affirmation. On conçoit très bien (pour moi quotidiennement) des matrices de définition de systèmes non linéaires! On les trouve même dans presque tous les domaines de la physique...
De même, il n'existe pas de contrainte théorique qui ferait qu'une matrice ne puisse être de dimension infinie!
Ce n'est pas parce que les matrices sont utilisées le plus souvent dans le secondaire et le premier cycle du supérieur pour décrire des applications linéaires dans des espaces vectoriels à dimension finie qu'il faut généraliser!
Alors pourquoi relier le concept de matrice, qui n'est qu'un outil de calcul, un moyen pratique de manipuler une grande quantité d'informations organisées, aux principes de finitude et de linéarité?
Par ailleurs, je trouve le titre du fil un peu tendancieux: "la matrice"! Cela rappelle le titre d'un film (évidemment) et aussi l'usage de ce mot pour définir autre chose que l'objet algébrique dont je parle.
Dans notre discours, si toutefois j'ai bien compris le sujet, on devrait parler d'algèbre des matrices plutôt que de "la matrice".
Dominique Lefebvre a écrit:En relisant ton post, Cesar, j'ai peut être mal compris quand tu écris que "c'est loin d'être une vérité absolue". Tu voulais peut être dire que les matrices ne sont pas forcément attachées aux systèmes linéaires et aux dimensions finies. Dans ce cas, j'abonde dans ton sens.
POur ce qui est des systemes linaires, j'entendais ceci, et rien d'autre : si A est une matrice et X et Y des vecteurs colonnes, r et s des scalaires, alors
A (r*X + s*Y) = r*A*X + s*A*Y
pour des systemes non lineaires, on ne peut, en general, utiliser les matrices que pour "l'étude locale", comme je l'ai déjà dit.
"On conçoit très bien (pour moi quotidiennement) des matrices de définition de systèmes non linéaires!" pourriez vous nous donner un exemple, afin que je sache si nous parlons bien de la meme chose ???
Bonsoir,
Dans l'étude du portrait de phase d'un système dynamique non linéaire, on peut être amené à linéariser autour d'un point critique pour étudier le comportement du système. On approxime le système non linéaire par un système différentiel linéaire au voisinage du point critique. On utilise donc des matrices (dans une approche linéaire, je te l'accorde).
Dans l'étude du comportement global des solutions, par exemple la recherche des bassins, des puits ou des sources, rien n'empêche de décrire un système non linéaire (si les fonctions sont lipschitziennes et au moins C2) par une écriture matricielle. Exemple simple: l'équation de Van der Pol...
Tout ça pour dire, que l'utilisation de matrice ne me fait pas particulièrement penser au monde linéaire.
D'ailleurs, j'en reviens à ma première question. En quoi un outil (ce qu'est l'algèbre matricielle) pourrait-il porter un concept philosophique? Parle-t-on de la philosophie d'un marteau ou d'une paire de pinces?
La seule fois où j'ai entendu mélée la philosophie aux matrices, c'est dans la naissance de la mécanique quantique (avec la mécanique des matrices de Heisenberg). Et encore, parler de philosophie est abusif. Il s'agissait plutôt d'épistémologie...
Dans l'étude du portrait de phase d'un système dynamique non linéaire, on peut être amené à linéariser autour d'un point critique pour étudier le comportement du système. On approxime le système non linéaire par un système différentiel linéaire au voisinage du point critique. On utilise donc des matrices (dans une approche linéaire, je te l'accorde).
Dans l'étude du comportement global des solutions, par exemple la recherche des bassins, des puits ou des sources, rien n'empêche de décrire un système non linéaire (si les fonctions sont lipschitziennes et au moins C2) par une écriture matricielle. Exemple simple: l'équation de Van der Pol...
Tout ça pour dire, que l'utilisation de matrice ne me fait pas particulièrement penser au monde linéaire.
D'ailleurs, j'en reviens à ma première question. En quoi un outil (ce qu'est l'algèbre matricielle) pourrait-il porter un concept philosophique? Parle-t-on de la philosophie d'un marteau ou d'une paire de pinces?
La seule fois où j'ai entendu mélée la philosophie aux matrices, c'est dans la naissance de la mécanique quantique (avec la mécanique des matrices de Heisenberg). Et encore, parler de philosophie est abusif. Il s'agissait plutôt d'épistémologie...
Dominique Lefebvre a écrit:Bonsoir,
Dans l'étude du portrait de phase d'un système dynamique non linéaire, on peut être amené à linéariser autour d'un point critique pour étudier le comportement du système. On approxime le système non linéaire par un système différentiel linéaire au voisinage du point critique. On utilise donc des matrices (dans une approche linéaire, je te l'accorde).
...
c'est ce que j'entends par étude locale. La matrice est incapable de resoudre globalement un systeme dynamique nonlineraire donné. D'ailleurs les fonctions analytiques existent t elles pour exprimer la solution....???
Pourquoi un outil serait t il porteur de philosophie, simplement d'apres moi, parce qu'il influence le raisonnement et la façon de penser. exemple, le livre : autrefois il se presentait sous forme de rouleaux, puis il s'est mis sous sa forme actuelle de codex. Cette transformation a influé directement sur le contenu de ce qui se trouvait écrit sur ses pages, en obligeant à le structurer de la maniere dont nous le connaissons. Aujourd'hui, avec l'informatique, une page de word se lit "en deroulé" comme les anciens rouleaux. On en retourne donc à la situation antiérieure, où la pensée était en quelque sorte plus linéaire, au lieu d'être hierarchisée...
bref, l'outil influe sur nos actions et nos pensées : sans ordinateur, pourriez vous calculer le bassin d'attraction d'un attracteur étrange ???
cesar a écrit:c'est ce que j'entends par étude locale. La matrice est incapable de resoudre globalement un systeme dynamique nonlineraire donné. D'ailleurs les fonctions analytiques existent t elles pour exprimer la solution....???
OK, on parle bien de la même chose... Tu sais, je rencontre rarement des systèmes qui présentent des solutions analytiques...
Pourquoi un outil serait t il porteur de philosophie, simplement d'apres moi, parce qu'il influence le raisonnement et la façon de penser. exemple, le livre : autrefois il se presentait sous forme de rouleaux, puis il s'est mis sous sa forme actuelle de codex. Cette transformation a influé directement sur le contenu de ce qui se trouvait écrit sur ses pages, en obligeant à le structurer de la maniere dont nous le connaissons. Aujourd'hui, avec l'informatique, une page de word se lit "en deroulé" comme les anciens rouleaux. On en retourne donc à la situation antiérieure, où la pensée était en quelque sorte plus linéaire, au lieu d'être hierarchisée...
bref, l'outil influe sur nos actions et nos pensées : sans ordinateur, pourriez vous calculer le bassin d'attraction d'un attracteur étrange ???
Je suis d'accord pour dire que l'outil influe sur la méthode voire sur la possibilité de développer la connaissance selon des axes qui seraient impossibles sans l'existence de ces outils... En effet, je vois mal mon job sans ordinateur....
Pour autant, l'ordinateur ne conditionne pas la nature de mon job. Je veux dire par là que, pour moi, l'outil ne transcende pas la nature (la philosophie) d'un système de connaissance.
Pour en revenir à notre débat, on peut disserter de la nature linéaire ou non linéaire de la nature . Ce peut être un débat philosophique (encore que le débat ne serait pas très original...). Mais le fait que l'on utilise les matrices pour travailler sur des systèmes linéaires ne me semble pas justifier que l'on considère l'algèbre matricielle comme de même nature philosophique.
Salut,
Même à un niveau élémentaire il est faux d'assimiler matrices et phénomènes linéaires. Je pense à la définition du corps des complexes telle qu'on l'enseignait dans les classes de terminale C dans les années 70.
Je me souviens très précisément du cours où on m'a présenté le corps des complexes. La prof commençait par étudier le corps des matrices réelles carrées (2,2) de forme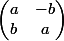 muni de l'addition et de la multiplication des matrices carrées. En passant elle nous a fait démontrer que R en était un sous-corps dont les éléments s'écrivaient
muni de l'addition et de la multiplication des matrices carrées. En passant elle nous a fait démontrer que R en était un sous-corps dont les éléments s'écrivaient 
Puis elle a démontré que ce corps était également un espace vectoriel sur R de dim 2 dont la base canonique s'écrivait (1,i).
Bref un ensemble de matrices suffisait à créer le corps des complexes. Le fait que i²=-1 n'était qu'une conséquence logique sans grande importance.
Il y avait dans cette approche une ambition démiurgique qui m'a marquée. Je crois devoir cet émerveillement aux matrices et je souhaite profiter de cette occasion pour les en remercier chaudement.
Même à un niveau élémentaire il est faux d'assimiler matrices et phénomènes linéaires. Je pense à la définition du corps des complexes telle qu'on l'enseignait dans les classes de terminale C dans les années 70.
Je me souviens très précisément du cours où on m'a présenté le corps des complexes. La prof commençait par étudier le corps des matrices réelles carrées (2,2) de forme
Puis elle a démontré que ce corps était également un espace vectoriel sur R de dim 2 dont la base canonique s'écrivait (1,i).
Bref un ensemble de matrices suffisait à créer le corps des complexes. Le fait que i²=-1 n'était qu'une conséquence logique sans grande importance.
Il y avait dans cette approche une ambition démiurgique qui m'a marquée. Je crois devoir cet émerveillement aux matrices et je souhaite profiter de cette occasion pour les en remercier chaudement.
bdupont a écrit:Salut,
Même à un niveau élémentaire il est faux d'assimiler matrices et phénomènes linéaires. Je pense à la définition du corps des complexes telle qu'on l'enseignait dans les classes de terminale C dans les années 70.
Je me souviens très précisément du cours où on m'a présenté le corps des complexes. La prof commençait par étudier le corps des matrices réelles carrées (2,2) de formemuni de l'addition et de la multiplication des matrices carrées. En passant elle nous a fait démontrer que R en était un sous-corps dont les éléments s'écrivaient
Puis elle a démontré que ce corps était également un espace vectoriel sur R de dim 2 dont la base canonique s'écrivait (1,i).
Bref un ensemble de matrices suffisait à créer le corps des complexes. Le fait que i²=-1 n'était qu'une conséquence logique sans grande importance.
Il y avait dans cette approche une ambition démiurgique qui m'a marquée. Je crois devoir cet émerveillement aux matrices et je souhaite profiter de cette occasion pour les en remercier chaudement.
l'exemple que vous donnez ne tient pas la route : c'est la linerarité qui permet cela ....
voici un extrait d'une etude sur la psycho du reve, notez les conclusions de l'auteur (je l'ai mise en gras)... la chose laisse pensif pas vrai ???
"Intermède mathématique
Une théorie représente une information sur un ensemble de faits et peut donc sexprimer par une fonction de type f = logx puisquune information prend toujours mathématiquement la forme dun logarithme. Si elle croise deux séries de faits, nous aurons f = logx et f = logy. Intégrer lensemble demande de faire F = logx + logy = logxy et non pas erreur plus classique quon ne pense log (x + y). Retraduite en langue du pays, cette loi mathématique de composition de linformation signifie quune théorie plus englobante ne peut se contenter de rabouter des morceaux de puzzle oubliés. Il faut forcément tout refondre et sattendre à ce que la nouvelle théorie permette des émergences imprévisibles par lune comme par lautre des théories de départ.
Dune certaine manière, pouvoir appliquer la théorie du signal à partir du simple constat de lexistence du rêve, et cela avant tout examen de son contenu, sapparente au passage à une théorie plus englobante. Du moins, cela nous permet de pointer les exigences auxquelles une théorie complète devrait répondre. Mais déjà à ce stade, nous pouvons supposer que cette théorie englobera davantage que le rêve lui-même. Notre réflexion incidente sur la ressemblance de la démarche de Freud avec celle de lécole de Copenhague nous a incité à voir si lon ne trouvait pas dautres faits de communication du même ordre entre physique et psychologie. Faute de données historiques consistantes, nous ne pouvons poursuivre lexploration en deçà du XVIIIe siècle.
Dates
Physique Psychologie
XVIIIe siècle Interactions de surface (modèle du billard) Homme insulaire, communication par les seuls organes sensoriels et le langage
1845 - 1848 Parson, découverte des nébuleuses spirales etidentification correcte comme galaxies.Les galaxies deviennent des objets autonomespar rapport aux étoiles Moreau de Tours : assimilation des rêves et des hallucinations,
découverte de lautonomie du psychisme.
1865 -1867 Maxwell : second principe de la thermodynamique appliqué aux gaz parfaits Hervey de Saint Denys : rêves
comme mélanges mémoriels. Premières notions de linconscient.
1900 Planck : découverte des quanta, les grains dénergie sont repérables par leurs effets mais au delà du mesurable. Freud : Linterprétation des rêves. Linconscient, hors de portée de
lobservation, révèle sa structure par ses effets.
1932 - 1935 Théorie quantique des champs. Découverte de leffet tunnel. Jung : première approche de linconscient collectif, qui agit comme un champ psychique.
1939 - 1942 Expérimentation sur la fission de latome. Débuts de la théorie de linformation. Les éléments constitutifs de la matière deviennent actifs dans le domaine macroscopique. Kilton Stewart : élaboration de la théorie senoï les éléments du rêve sont actifs jusque dans la vie de veille et non seulement révélateurs de la psyché.
1951 - 1952 Méthode de comptage des particules parscintillation. Chambre à bulles. Maser.Structure fine de la matière. Kleitman et Aserinsky : à partir de lEEG, découverte de la structure du sommeil.
1970 Hawking : évaporation du trou noir Découverte de lexistence dune forme de communication chez les autistes et les catatoniques
1973 - 1974 Maîtrise de la fission nucléaire, premières piles industrielles Travaux dUllman et Krippner.
Publication de louvrage de Patricia Garfield sur le rêve lucide et la méthode senoï : maîtrise du rêve.
1978 - 1980 Prigogine et Stengers : thermodynamique chaotique. Théorie inflatoire. Stephen LaBerge et, indépendam ment, Alan Worsley : communiction directe par signaux oculaires entre un rêveur et un appareil de mesure.
1982 Mise sur pied du Projet Sigma de détection des trous noirs, jusquici objets prévus par la théorie mais à lexistence concrète douteuse. Premier rêve mondial, dans lequel lidée est lancée sans réelle réalisation.
1990 Lancement de Sigma Rêve planétaire, réalisé à grande échelle
1991 Janvier : découverte du trou noir Nova Muscae Début de lannée : mise en évidence dun mythème accréditant lhypothèse de linconscient collectif
1996 Généralisation des recherches de Sigma existence de novae à trous noirs dans le bulbe galactique. Les trous noirs cessent dêtre des objets purement théoriques. Etude globale du rêve planétaire, mise en évidence dindices donnant
une consistance expérimentale à linconscient collectif.
Ce qui frappe à la lecture de ce tableau, cest lémergence de modèles du même type au même moment dans des sciences réputées se placer aux deux extrémités du spectre. Une étude fine montrerait sans doute une partie des voies de transmission de linformation, tout du moins de conscient à conscient. Mais le seul fait davoir pu réaliser cette étude sommaire montre quil y a intercommunication et quelle dépasse sans doute le conscient des chercheurs. Lorsque le premier projet de rêve mondial a été lancé, le projet Sigma était encore considéré comme secret. Dautre part, étant donné les préjugés de boutique, il est inconcevable dès la fin du XVIIIe siècle quun physicien aille chercher consciemment des idées et des modèles dans les sciences humaines ; et de nombreux indices tendraient à prouver que les psychologues leur rendent bien leur ignorance"
"Intermède mathématique
Une théorie représente une information sur un ensemble de faits et peut donc sexprimer par une fonction de type f = logx puisquune information prend toujours mathématiquement la forme dun logarithme. Si elle croise deux séries de faits, nous aurons f = logx et f = logy. Intégrer lensemble demande de faire F = logx + logy = logxy et non pas erreur plus classique quon ne pense log (x + y). Retraduite en langue du pays, cette loi mathématique de composition de linformation signifie quune théorie plus englobante ne peut se contenter de rabouter des morceaux de puzzle oubliés. Il faut forcément tout refondre et sattendre à ce que la nouvelle théorie permette des émergences imprévisibles par lune comme par lautre des théories de départ.
Dune certaine manière, pouvoir appliquer la théorie du signal à partir du simple constat de lexistence du rêve, et cela avant tout examen de son contenu, sapparente au passage à une théorie plus englobante. Du moins, cela nous permet de pointer les exigences auxquelles une théorie complète devrait répondre. Mais déjà à ce stade, nous pouvons supposer que cette théorie englobera davantage que le rêve lui-même. Notre réflexion incidente sur la ressemblance de la démarche de Freud avec celle de lécole de Copenhague nous a incité à voir si lon ne trouvait pas dautres faits de communication du même ordre entre physique et psychologie. Faute de données historiques consistantes, nous ne pouvons poursuivre lexploration en deçà du XVIIIe siècle.
Dates
Physique Psychologie
XVIIIe siècle Interactions de surface (modèle du billard) Homme insulaire, communication par les seuls organes sensoriels et le langage
1845 - 1848 Parson, découverte des nébuleuses spirales etidentification correcte comme galaxies.Les galaxies deviennent des objets autonomespar rapport aux étoiles Moreau de Tours : assimilation des rêves et des hallucinations,
découverte de lautonomie du psychisme.
1865 -1867 Maxwell : second principe de la thermodynamique appliqué aux gaz parfaits Hervey de Saint Denys : rêves
comme mélanges mémoriels. Premières notions de linconscient.
1900 Planck : découverte des quanta, les grains dénergie sont repérables par leurs effets mais au delà du mesurable. Freud : Linterprétation des rêves. Linconscient, hors de portée de
lobservation, révèle sa structure par ses effets.
1932 - 1935 Théorie quantique des champs. Découverte de leffet tunnel. Jung : première approche de linconscient collectif, qui agit comme un champ psychique.
1939 - 1942 Expérimentation sur la fission de latome. Débuts de la théorie de linformation. Les éléments constitutifs de la matière deviennent actifs dans le domaine macroscopique. Kilton Stewart : élaboration de la théorie senoï les éléments du rêve sont actifs jusque dans la vie de veille et non seulement révélateurs de la psyché.
1951 - 1952 Méthode de comptage des particules parscintillation. Chambre à bulles. Maser.Structure fine de la matière. Kleitman et Aserinsky : à partir de lEEG, découverte de la structure du sommeil.
1970 Hawking : évaporation du trou noir Découverte de lexistence dune forme de communication chez les autistes et les catatoniques
1973 - 1974 Maîtrise de la fission nucléaire, premières piles industrielles Travaux dUllman et Krippner.
Publication de louvrage de Patricia Garfield sur le rêve lucide et la méthode senoï : maîtrise du rêve.
1978 - 1980 Prigogine et Stengers : thermodynamique chaotique. Théorie inflatoire. Stephen LaBerge et, indépendam ment, Alan Worsley : communiction directe par signaux oculaires entre un rêveur et un appareil de mesure.
1982 Mise sur pied du Projet Sigma de détection des trous noirs, jusquici objets prévus par la théorie mais à lexistence concrète douteuse. Premier rêve mondial, dans lequel lidée est lancée sans réelle réalisation.
1990 Lancement de Sigma Rêve planétaire, réalisé à grande échelle
1991 Janvier : découverte du trou noir Nova Muscae Début de lannée : mise en évidence dun mythème accréditant lhypothèse de linconscient collectif
1996 Généralisation des recherches de Sigma existence de novae à trous noirs dans le bulbe galactique. Les trous noirs cessent dêtre des objets purement théoriques. Etude globale du rêve planétaire, mise en évidence dindices donnant
une consistance expérimentale à linconscient collectif.
Ce qui frappe à la lecture de ce tableau, cest lémergence de modèles du même type au même moment dans des sciences réputées se placer aux deux extrémités du spectre. Une étude fine montrerait sans doute une partie des voies de transmission de linformation, tout du moins de conscient à conscient. Mais le seul fait davoir pu réaliser cette étude sommaire montre quil y a intercommunication et quelle dépasse sans doute le conscient des chercheurs. Lorsque le premier projet de rêve mondial a été lancé, le projet Sigma était encore considéré comme secret. Dautre part, étant donné les préjugés de boutique, il est inconcevable dès la fin du XVIIIe siècle quun physicien aille chercher consciemment des idées et des modèles dans les sciences humaines ; et de nombreux indices tendraient à prouver que les psychologues leur rendent bien leur ignorance"
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
