Pafapafadidel a écrit:En ramenant l'étude des inverses a gauche de x a celle des diviseurs de 0 a gauche de x, j'arrive a prouver qu'ils sont tous inverses a gauches et deux a deux distincts. De plus, je pense avoir réussi a prouver que tous les inverses a gauche de x sont de la forme y+a(1-xy) (en quotientant A par l'idéal a gauche engendré par (1-xy) et en vérifiant que tous les diviseurs de 0 de x a gauche appartiennent a cet idéal).
C'est parfaitement O.K.
Dans la preuve, il n'est pas vraiment utile de quotienter A par un idéal à gauche (le résultat n'est plus un anneau : il faut quotienter par un idéal bilatère pour que le quotient soit un anneau).
En fait il suffit d'écrire
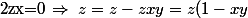)
pour montrer que les diviseurs de 0 à gauche de
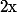
sont de la forme
)
Pafapafadidel a écrit:Pour "l'unicité" par contre, je suis completement perdu. Je pense avoir une piste en montrant que les diviseurs de 0 a gauche de (1-xy) sont de la forme
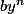
avec a non diviseur de 0 a gauche de (1-xy).
Là, je ne vois pas trop ce que tu cherche à faire...
Je pense que tu as mal compris ce que disait kazeriahm dans son premier post : les
)
sont bien des inverses à gauche de
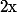
distincts, mais ce ne sont pas forcément
les seuls inverses à gauche de
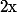
.
Pour t'en convaincre, regarde sur un exemple :
Soit
})
l'espace vectoriel formé des suites réelles dont tout les termes sont nuls à partir d'un certain rang.
On prend pour
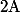
l'anneau des endomorphismes de
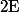
et on considère les éléments suivants de
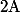
:
\mapsto(0,u_0,u_1,u_2,...))
\mapsto(u_1,u_2,u_3,u_4,...))
Vérifie que
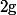
et un inverse à gauche de
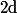
puis que les inverse à gauche de
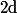
ne sont pas tous de la forme
)
 , si un élément
, si un élément  a un inverse à gauche et aucun inverse à droite, alors
a un inverse à gauche et aucun inverse à droite, alors  a une infinité d'inverse à gauche, donnés par la suite de terme général
a une infinité d'inverse à gauche, donnés par la suite de terme général ,
, 
