Intersection d'ensembles infinis

[Ben314]

Salut,
C'est quoi l'intersection de l'ensemble des entiers naturels pairs et de l'ensemble des nombres premiers ?

[nodjim]

C'est pas vide, il y a 2. C'est Ben314 qui l'a écrit, il faut faire attention quand il écrit, car rarement faux.

[Waax22951]

Super ! Merci Ben. Est-ce qu'il y en a d'autres ?

En fait, en reprenant l'exemple de Ben, pour tout nombre premier , on a:
[CENTER][/CENTER]

Où P est l'ensemble des nombres premiers. :we:

Bonne journée ! :lol3:

[Ben314]

Visiblement, tu ne semble pas très familier avec la notion "d'ensemble" : il y a évidement d'autres exemples et en fait tu peut (évidement) obtenir absolument n'importe quoi comme intersection de deux ensembles infinis.
Si on prend une partie C absolument quelconque de N puis qu'on prend comme ensemble A la réunion de C et de l'ensemble des nombres pairs et qu'on prend comme ensemble B la réunion de C et de l'ensemble des nombres impairs.
Alors A et B seront clairement infini et, tout aussi clairement, leur intersection sera l'ensemble C de départ qui était... quelconque (vide ou fini non vide ou, infini, enfin n'importe quoi....)

[nodjim]

Pour archiM: un ensemble ne se caractérise pas forcément par une propriété (pair, premier, carré,...). Il peut se définir par une liste entièrement ou partiellement.
Exemple: ensemble des entiers pairs et le nombre 15.
A partir de là tu comprends bien qu'on peut facilement trouver ce que tu cherches.

[Monsieur23]

Aloha,

Si B est inclu dans A, l'intersection de A et B, c'est B, non ? Donc infinie ?

[Monsieur23]

Merci, c'est évident.
Je repose correctement (!) mon problème.
A et B sont infinis. Pour C, je ne sais pas.
A contient B, B contient C.
A inter B (B) est donc infini, on l'a dit.
Comment savoir si B inter C (C) est infini ?

Dans ton exemple, A et B ne servent "à rien", et donc ta question revient à "J'ai un ensemble C, comment je peux savoir s'il est fini ou infini ?". Il n'y a pas de réponse canonique à ça, ça dépend des cas.

[Ben314]

Pour te donner une analogie, c'est comme si tu disait :
J'ai un réel inconnu x. Je sais qu'il est inférieur à 10 et je sais que 10 est inférieur à 17.
Comment savoir si x est plus grand que 5 ou pas ?

[Ben314]

Non, c'est différent, vu que cette fois, c'est comme si tu disait que tu prend .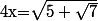
Là, on connait x donc on peut assez surement dire s'il est ou pas supérieur à 5.
Et, évidement, la méthode pour savoir si c'est vrai ou pas va... dépendre de ce qu'on a comme info. sur x : j'espère que tu sait qu'il n'y a pas de "méthode à appliquer à tout les coups" pour montrer qu'un truc est supérieur à 5.

Dans ton cas, par exemple, c'est assez évident : le carré de tout nombre pair est (évidement) un carré ET c'est un nombre pair.
Donc il y a une infinité de carrés pairs.