Intégrale de différence angulaire ?

[TheReveller]

Bonjour,

J'aimerais savoir s'il est possible de définir une fonction f(s,d) qui, pour une courbe paramétrée en longueur d'arc (s), renvoiera la sommation des différences angulaires pour tous les ds de s à s+d.

Grossièrement, lorsque je cherche f(s=5,d=2), je cherche à déterminer la sommation des différences d'angle entre les normales à [5 et 5+ds], [5+ds et 5+2*ds], ..., [5+n*ds et 5+2]

Le cas simple à vérifier serait que pour tout cercle paramétré en longueur d'arc (donc le cercle est défini en entier lorsqu'on trace s de 0 à 2*pi*a), on obtiendrait par exemple un total de 360 degrés pour f(s=0,d=2*pi*a), ou par exemple un total de 45 degrés pour f(s=0,d=2*pi*a/8), etc. Et bien entendu, pour une ligne droite, la fonction renvoie toujours 0.

Merci,

Éric

[Ben314]

Salut,
Je suis pas sûr de très bien comprendre ta question....
Si on regarde ta courbe à valeur dans C (plutôt que R^2), comme elle est parcourue à vitesse constante, est un point du cercle trigo. donc et il y a un théorème un peu costaud qui dit que, si est continue, alors il existe une fonction continue vérifiant le truc en question.
Dans ce cas, si je comprend bien, ton , ça serait = différence d'angle entre les vecteurs tangents en s et en s+d (= idem pour les vecteurs normaux qui font un angle de pi/2 avec les vecteurs tangents)

Après, dans un cadre théorique, si tu veut une formule plus ou moins explicite donnant ton , tu as ça :

Qui peut se retranscrire si tu le souhaite en terme d'intégrales purement réelles portant sur les coordonnées x(s) et y(s) de voire même dans le cas de courbes non p.l.a.

[TheReveller]

Ça m'intéresse, j'aimerais plus de détails.

Je vais tenter de reformuler ma question en plus simple.

Disons que j'ai une courbe paramétrée en s ([longueur d'arc] ou sinon en t "temps"). Maintenant disons que je prends un bout de cette courbe et que je la divise infiniment en parties égales. Pour chaque subdivision, je calcule la différence d'angle entre la normale à ce point et la normale au point suivant (qui est à une distance infinitésimale).

Bref, c'est comme si je prenais pas exemple un cercle et que je le divisais en 10. La différence d'angle entre chacune des normales à ces points serait 36 degrés, totalisant 360 degrés pour le cercle en entier. Si je le divise en 360, alors 1 degré, et ainsi de suite jusqu'à la limite où l'angle s'approche de 0. Un peu comme lorsqu'on calcule la longueur d'arc entre a et b, on somme toutes les petites distances infinitésimales, mais cette fois on somme toutes les petites différences d'angle infinitésimales.

Merci!

[Ben314]

Alors, c'est clair (il me semble) :

Pour une paramétrisation quelconque,

ça te donne la variation d'angle (sur le cercle osculateur) pour une variation de temps de 1 et tu peut parfaitement l'intégrer "en dt", ça donnera la variation d'angle entre les vecteur correspondant aux bornes de ton intégrale.

ça te donne la variation d'angle (sur le cercle osculateur) pour une variation de distance de 1 et de l'intégrer "en dt", ça ne veut rien dire (sauf si tu as une p.l.a. où t=s et dt=ds)

[TheReveller]

Merci, jusqu'à maintenant ça semble effectivement être exactement ce que je recherchais!

Est-ce que je peux avoir le nom de cette formule pour que je puisse comprendre par sa démonstration ?

J'étais rendu à quelque chose de similaire par produit scalaire.

Si je veux que la somme ne soit qu’additive (pas d'angles négatifs), je n'ai qu'à intégrer sur la valeur absolue ?

Merci beaucoup!

[Ben314]

Je ne pense pas que la formule en question porte de nom.
C'est à peu de chose prés le calcul de la courbure d'un arc et c'est donc plus plus ou moins lié a la notion de repère de Frenet

Après, peut-être que sur certaines applications pratique cela a du sens de calculer l'intégrale de la valeur absolue du truc, mais en math., tu va perdre un grand nombre de propriétés (par exemple le fait que sur un lacet complet, l'intégrale vaut 2k.pi avec k entier)

Grosso modo, le calcul en valeur absolue correspond à dire que, si on tourne à droite de 15° puis à gauche de 20° alors on tourne "au total" de 35° et il ne me semble pas que ce 35° représente grand chose (alors que 20°-15° lui représente quelque chose)

[TheReveller]

Je ne pense pas que la formule en question porte de nom.
C'est à peu de chose prés le calcul de la courbure d'un arc et c'est donc plus plus ou moins lié a la notion de repère de Frenet

Après, peut-être que sur certaines applications pratique cela a du sens de calculer l'intégrale de la valeur absolue du truc, mais en math., tu va perdre un grand nombre de propriétés (par exemple le fait que sur un lacet complet, l'intégrale vaut 2k.pi avec k entier)

Grosso modo, le calcul en valeur absolue correspond à dire que, si on tourne à droite de 15° puis à gauche de 20° alors on tourne "au total" de 35° et il ne me semble pas que ce 35° représente grand chose (alors que 20°-15° lui représente quelque chose)

Merci! En fait, je voulais comprendre un peu ce qui t'as mené à cette formule.

Pour la valeur absolue, c'est parce que si je parcours un sinus, alors on dira après une période que le total est 0 degré. Pour ton explication, c'est vrai que ça signifie alors qu'on a autant tourné d'un sens que dans l'autre, mais je m'intéresse à avoir un indice totalisant toutes les fois où on a eu à tourner pour pas qu'un sinusoïde de A à B donne 0 au même titre qu'une ligne droite de A à B.

Merci encore!

Edit : Ah, voilà, sur la page Wikipédia de la courbure d'un arc que tu m'as envoyée, je vois les formules de courbures pour un graphe et une courbe paramétrée et je connais très bien ces formules. Je cherchais justement le lien entre la différence d'angle locale à un point et la courbure, je vais pouvoir partir de là, ce n'est qu'un exposant de différence. Merci pour l'information sur le repère de Frenet, je vais lire ça!

[TheReveller]

Rebonjour,

J'ai un questionnement.

Dans les formules que tu as fournies, tu m'as dit que la première est pour une paramétrisation par longueur d'arc et la seconde pour une paramétrisation quelconque.

Je viens d'effectuer un test qui m'a posé problème.

Disons que j'ai une spirale logarithmique x(t) = e^t*cos(t) et y(t) = e^t*sin(t) et que j’utilise la seconde formule puisque j’ai une paramétrisation quelconque. Si je n’utilise pas l’intégrale, mais simplement la formule pour évaluer l’angle local à un point t, j’obtiens une valeur constante pour tout t. Or, la courbure est de plus en plus faible, donc l’angle local devrait être de plus en plus faible, mais ce n’est pas le cas.

Peut-être qu’il y a erreur dans mes calculs.

Par contre, si je convertis en paramétrisation par longueur d’arc [ x(t) = e^(ln((t+1)^2)/2)*cos(ln((t+1)^2)/2) et y(t) = e^(ln((t+1)^2)/2)*sin(ln((t+1)^2)/2) ], alors j’obtiens un angle décroissant comme désiré. Cependant, bien que la première et la deuxième formule aient alors la même forme avec cette paramétrisation, elles ne donnent pas les mêmes valeurs. Peut-être pourras-tu m’éclairer ?

Voici un lien explicatif visuellement : https://www.desmos.com/calculator/mxgkqoopa5

PS : Oui, e^(ln((t+1)^2)/2) = t+1, je n'ai pas simplifié pour garder la trace du changement par substitution de variable.

Merci !

[Ben314]

Oui, effectivement, le truc que je t'ai donné, ce n'est pas la courbure (pour la courbure, il faut mettre un exposant 3/2 sur le dénominateur)
Mais j'avais cru comprendre à travers l'exemple du cercle que tu donnait que ce qui t'intéressait, c'était uniquement la variation d'angle et pas la courbure.
Par exemple, dans le cas de x=e^t.cos(t) et y=e^t.sin(t) si tu regarde l'angle entre le vecteur vitesse au temps t et le vecteur vitesse au temps t+epsilon, il est exactement égal à epsilon (et ne dépend pas de t).
C'est tout a fait cohérent avec le fait que la courbure soit de plus en plus faible vu que, la distance parcourue entre t et t+epsilon et de plus en plus grande lorsque t augmente. Donc on a toujours la même différence d'angle mais pour une distance parcourue de plus en plus grande => une courbure de plus en plus faible (il faut plus tourner pour faire demi tour sur un parcours de 50m que pour pour faire demi tour sur un parcours de 200m)

Mais après, c'est peut être autre que la variation d'angle que tu veut mesurer...

[TheReveller]

Je m'intéresse effectivement à la variation d'angle. En fait, je suis un peu mélangé avec le cas de la spirale, je ne suis plus certain de ce que je veux (alors j'aimerais démêler tous les cas et leurs explications) parce que je ne comprends pas pourquoi une spirale aurait localement une différence d'angle constante au même titre qu'une spirale.

En fait, non, je crois que je comprends, c'est que pour le cercle le ds parcouru est constant par rapport à dt alors que pour la spirale le ds parcouru augmente par rapport à dt.

Bref, ce que j'ai compris avec la spirale, c'est que la variation d'angle est constante puisque la différence d'angle entre le temps t et t+1 est la même. Et cette différence est la même puisque la longueur d'arc entre t et t+1 augmente de plus en plus.

Or, je croyais que la deuxième formule annulait cet effet de variation de longueur d'arc de telle sorte qu'on mesure la différence d'angle entre s et s+1. C'est là mon problème. Comment, à partir de la formule pour une paramétrisation quelconque, pourrais-je obtenir la variation entre s et s+1, bref la variation en angle en fonction de la distance et non du temps?

En fait, les deux m'intéressent, mais j'aimerais savoir laquelle est laquelle puisque là j'ai en quelque sorte 4 formules : la première et la deuxième version (sans et avec dénominateur) lorsqu'appliquées à une courbe de paramétrisation quelconque et la première et la deuxième version (sans et avec dénominateur) lorsqu'appliquées à une courbe de paramétrisation par longueur d'arc. Et dans aucun cas je n'ai celle qui fournit la réponse par ds à partir d'une paramétrisation quelconque.

Et pourquoi ma courbe g du lien que j'ai fourni ne donne pas le même résultat (vert et bleu) alors qu'elle est paramétrée par longueur d'arc.

Merci mille fois!

[Ben314]

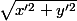
Si tu veut évaluer (localement) la variation d'angle par rapport à la distance parcourue (et pas par rapport au temps), il faut effectivement que tu divise par la vitesse, c'est à dire par ce qui fait que maintenant, tu as un exposant 3/2 sur le dénominateur et tu retombe sur la notion usuelle de courbure (qui mesure bien la variation d'angle par rapport à la distance parcourue).

Par contre, si tu intègre ça entre t1 et t2 (pour une paramétrisation non p.l.a) je pense que le résultat ne correspond à rien de géométrique vu que tu intègre en t (donc par rapport au temps) un truc qui est une variation d'angle par rapport à la distance parcouru...


Après, tes courbe bleu et rouge, si elle correspondent au calcul avec un dénominateur "simple" (donc sans la puissance 3/2), c'est normal qu'elle ne coïncident pas vu qu'elles représente la variation d'angle par rapport au temps et donc, les valeurs sont différentes lorsque l'on parcours la même courbe à des vitesses différentes.

Là où il faudrait que ce soit clair, c'est qu'avec ton histoire d'intégrale, ça me donnait l'impression que tu cherchait à définir un truc entre deux points éventuellement assez éloignés de la courbe (en t et en t+t'). Je pensait que c'était l'angle entre les vecteurs directeurs (ou les vecteurs normaux, c'est la même chose) mais en fait, ça n'a pas l'air d'être ça.
Dans le cas par exemple d'une spirale sur laquelle on prend deux points (un peu éloignés) tu cherche à mesurer quoi en fait ?

[TheReveller]

Je m'attends par exemple à ce que pour une même paramétrisation de la courbe de formule :

x(t) = a*cos(t)
y(t) = a*sin(t)

Une formule me donne 2*pi = 360 degrés pour une intégrale de 0 à 2*pi (version temps) et une autre formule me donne également 2*pi = 360 degrés pour une intégrale de 0 à 2*pi*a (version distance).

On a déjà la version temps, c'est la deuxième version (celle généralisée) de la formule que tu m'as fournie.

Edit : Oh, la version distance serait d'intégrer sur la formule de courbure (avec l'exposant 3/2)? Je viens de tester avec un cercle et ça fonctionne...

Edit : Pour me problème de courbes qui ne correspondent pas, ce sont les courbes vertes et bleues. Les deux sont basées sur g qui est paramétrée par longueur d'arc, donc elles devraient donner le même résultat, mais pour une raison dont j'ignore le dénominateur vaut 2 au lieu de 1... Erreur de calcul de ma part ?

Edit : Et l'interprétation à donner à ces formules (lorsqu'évaluées en un point et non en intégrale), c'est la différence d'angle "f(p)" qu'on aurait par rapport au point "p" si on avait parcouru une unité de [temps ou distance] (selon la formule) dans cette même direction angulaire en imaginant un cercle osculateur (bref ça fonctionne pour le cercle, l'intégrale de 0 à 1 est égale à la valeur à f(0)). Hmm, je ne crois pas que ce soit clair, mais je me comprends.

[Ben314]

Alors, c'est clair (il me semble) :

Pour une paramétrisation quelconque,

ça te donne la variation d'angle (sur le cercle osculateur) pour une variation de temps de 1 et tu peut parfaitement l'intégrer "en dt", ça donnera la variation d'angle entre les vecteur correspondant aux bornes de ton intégrale.

ça te donne la variation d'angle (sur le cercle osculateur) pour une variation de distance de 1 : c'est ce qu'on appelle "la courbure" et c'est l'inverse du rayon du cercle osculateur.
Par contre, de l'intégrer "en dt", ça ne veut rien dire sauf si tu as une p.l.a. où t=s et dt=ds mais comme dans ce cas , c'est (heureusement) la même chose que la première formule.

[TheReveller]

Alors, c'est clair (il me semble) :

Pour une paramétrisation quelconque,

ça te donne la variation d'angle (sur le cercle osculateur) pour une variation de temps de 1 et tu peut parfaitement l'intégrer "en dt", ça donnera la variation d'angle entre les vecteur correspondant aux bornes de ton intégrale.

ça te donne la variation d'angle (sur le cercle osculateur) pour une variation de distance de 1 : c'est ce qu'on appelle "la courbure" et c'est l'inverse du rayon du cercle osculateur.
Par contre, de l'intégrer "en dt", ça ne veut rien dire sauf si tu as une p.l.a. où t=s et dt=ds mais comme dans ce cas , c'est (heureusement) la même chose que la première formule.

Tout est clair! Merci beaucoup de ton aide, c'est très apprécié!