Impossible

[maxence6]

Bonjour je me demandé si on pouvait affirmer qu'un nombre est nul si dans une équation on tombe sur quelque chose comme sa:



Je pense que oui car s'il n'est pas nul l'égalité est fausse !

Explications:

donc on peut écrire




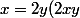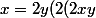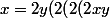Et si on continu il peut être infiniment grand enfin plutôt infiniment "error" car un nombre de peut pas être égal par exemple a son triple.

Donc peut on affirmé que x=0 dans ce cas ?

[Skullkid]

Si y = 1/2 alors x peut avoir n'importe quelle valeur. En revanche, si y est différent de 1/2, alors x = 0.

Pour la démo :

x = 2xy <=> x(2y-1) = 0 et un produit est nul si et seulement si l'un des facteurs est nul.

Sinon, ta suite d'égalités est fausse : sur la fin tu remplaces x par 2x au lieu de 2xy

[maxence6]

Oki Merci !