Groupes quotients isomorphes

[Richard532]

Bonjour, je me permets de partager une question :
Soient des groupes tels que et .
A-t-on alors : ?

En claire, j'ai remarqué au cours d'un exercice sur les isomorphismes de groupe (en L3 math) que on avait :
Avec un groupe multiplicatif.
et ---ainsi que--- et

J'aurais voulu savoir s'il était possible d'en faire une généralité.

Merci d'avance si quelqu'un a une piste

[GaBuZoMeu]

As tu déjà pratiqué la chasse au diagramme ?



Sinon, c'est une bonne occasion pour commencer. J'attends une réaction.

[GaBuZoMeu]

Richard 532 serait-il victime d'une balle perdue de la chasse au diagramme ?

Pour qu'on voie comment ça fonctionne, je vais faire le bout facile. Je suppose que le morphisme canonique est un isomorphisme, et je montre que est injectif
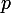
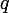
Soit qui s'envoie sur l'élément neutre 1 de . Je relève en un ; soit l'image de . L'image de dans est 1 (commutativité du diagramme), donc vient d'un .
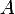
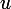
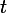
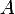
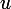
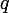
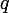
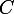
L'image de dans est 1, car vient d'un élément de . L'image de dans est aussi 1, par l'hypothèse que est un iso. Donc vient d'un . Soit l'image de dans . Alors et ont même image par et donc puisque est injectif. Ainsi vient de et donc son image est égale à 1. Ceci montre que le noyau de est réduit à l'élément neutre.

On a chassé dans tout le diagramme. Je laisse d'autres chasseurs montrer que est surjectif.