Groupe

[amine801]

salut tout le monde
Soit G un groupe muni d’une loi de composition interne(*)
soit
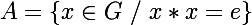
(e Désigne l'element neutre)
que pensez vous de l’affirmation suivante:

vrai ou faux?
bonne réflexion :party:

[fahr451]

bonjour

il manque des quantificateurs

est ce pour tout groupe G on a , A = {e} (1)
ou il existe un groupe G tel que A = {e} ? (2)

(1) est fausse prendre E un ensemble non vide et G = P(E) muni de delta
on a A = G ;ou G= {-1,1} muni de la multiplication


(2) est vraie prendre G = {e}

[amine801]

bonjour,
C’était un post pour m’insurger contre l’aspect binaire de certain esprit ainsi
La théorie des groupes est un système axiomatique incomplet est la propriété ne peut être vraie ou fausse à moins d’avoir un modèle.

[abcd22]

Et le post ci-dessus c'était juste pour caser quelques mots de logique ?

[amine801]

Non Juste pour avoir la réponse ci-dessus :zen:

[cesar]

bonjour,
C’était un post pour m’insurger contre l’aspect binaire de certain esprit ainsi
La théorie des groupes est un système axiomatique incomplet est la propriété ne peut être vraie ou fausse à moins d’avoir un modèle.

que la theorie soit incomplete, on le sait depuis godel et son theoreme - le theories mathematiques sont essentiellement incompletes -.... mais tu n'as pas prouvé que l'on était sur un cas d'incompletude...tu l'as dit, mais tu ne l'as pas prouvé...fahr451 a meme prouvé que cela dependait du groupe considéré... donc que l'on pouvait décider au cas par cas.... bref, ce n'est pas une "vraie" indécidable.

c'est bien dommage : lorsqu'on trouve un cas de ce genre, on ouvre la porte a une theorie nouvelle....
le cas probablement le plus celebre : celui de l'axiome d'euclide dont l'examen du caractere indecidable a ouvert la route vers la geometrie Riemanienne...