Formes quadratiques / Gram-Schmidt

[UG8B8SS]

Bonjour j’ai un peu de mal concernant une évaluation passée

Voici l’exercice :
Soit q une forme quadratique de R4 vers R
tel que q(x,y,z,t) = x^2 -2y^2 -2t^2 + 2xz + 4xt + 2yz - 2zt

Q1) donner la matrice A de q et donner des mineurs principaux

Là dessus pas trop de problème je pense avoir bon voici la matrice

1 0 1 2
0 -2 1 0
1 1 0 -1
2 0 -1 -2

Et les mineurs me donne que q change de signe d’après le critère de Sylvester

Q2) en vérifiant que la méthode de Gram-Schmidt s’applique, trouver la forme diagonale de q et donner sa signature

C’est là où je bloque ..
J’aimerai bien une correction si possible

[Ben314]

Salut,
à une petite exception prés (où on écrit que ) Gram-Schmidt c'est jamais que la bonne vieille mise sous forme canonique d'un trinôme vue et revue au Lycée :
Si on commence par les , on dit que les termes dépendant de , c'est à dire c'est le début du carré de et on ajoute (et retranche) ce qu'il faut, c'est à dire 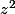pour que ça fasse un carré parfait.
Puis on recommence avec les autres variables.
Et si à la fin, tu n'a plus aucun carré pour faire tes début d'identité remarquable, tu utilise l'astuce que j'ai mise entre parenthèse au début.