Racine (2n^4 +3n^2) -Racine (2n^4-3n^2)
Si vous avez des idées, n’hesitez pas
Forme indéterminée avec racines
3 messages
- Page 1 sur 1
Forme indéterminée avec racines
par Megapix31 » 05 Nov 2019, 21:25
Bonjour à tous, je cherche à trouver la limite de la suite suivante pour n>=3 :
Racine (2n^4 +3n^2) -Racine (2n^4-3n^2)
Si vous avez des idées, n’hesitez pas
Racine (2n^4 +3n^2) -Racine (2n^4-3n^2)
Si vous avez des idées, n’hesitez pas
Re: Forme indéterminée avec racines
par capitaine nuggets » 05 Nov 2019, 21:45
Salut !
Peut-être en utilisant la quantité conjuguée : pour tous réels
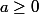
et 
tels que a et b ne soient pas simultanément nuls, tu as :
(\sqrt a + \sqrt b)}{\sqrt a + \sqrt b} = \frac{ ({\sqrt a})^2- (\sqrt b)^2 }{\sqrt a + \sqrt b} = \frac{ a- b }{\sqrt a + \sqrt b})
.
Ici, tu as pour tout
:
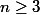
}{\sqrt{2n^4+3n^2}+ \sqrt{2n^4-3n^2}})
Peut-être en utilisant la quantité conjuguée : pour tous réels
Ici, tu as pour tout
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :