Fonction à répartition décroissante à somme borné
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
ncrroger
- Messages: 5
- Enregistré le: 06 Juin 2017, 14:55
-
 par ncrroger » 06 Juin 2017, 15:12
par ncrroger » 06 Juin 2017, 15:12
Bonjour,
je suis à la recherche d'une fonction de répartition (désolé si je me trompe sur le nom) décroissante à somme borné tel que
 \geq f(i+1))
et
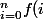 \leq a)
où
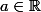
et est fini et connu

et est fini et connu
Merci à tous pour votre aide
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 07 Juin 2017, 17:00
par nodgim » 07 Juin 2017, 17:00
Par exemple f(i) = 1/1² + 1/2² + ....1/i² ?
-
ncrroger
- Messages: 5
- Enregistré le: 06 Juin 2017, 14:55
-
 par ncrroger » 07 Juin 2017, 19:27
par ncrroger » 07 Juin 2017, 19:27
Merci pour ta réponse, mais cette fonction ne réparti pas bien. Je voudrai une fonction qui pourrait par exemple répartir 5 à 15 personne de manière à ce que la première personne est plus que la suivante et ainsi de suite et que les avoirs soit linéairement décroissant si possible (mais c'est pas obligatoire).
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 07 Juin 2017, 19:55
par pascal16 » 07 Juin 2017, 19:55
tu peu aussi voir ça comme une suite
U0= k (k entre 0 et 1)
Un+1 = Un - p (p positif)
et on calcule p avec le somme des termes d'une suite arithmétique qui doit valoir 1
c'est décroissant, linéaire et normé pour de la proba
-
ncrroger
- Messages: 5
- Enregistré le: 06 Juin 2017, 14:55
-
 par ncrroger » 07 Juin 2017, 19:57
par ncrroger » 07 Juin 2017, 19:57
Merci je vais exploré cette piste
-
ncrroger
- Messages: 5
- Enregistré le: 06 Juin 2017, 14:55
-
 par ncrroger » 08 Juin 2017, 07:14
par ncrroger » 08 Juin 2017, 07:14
la suite marche bien, Merci @pascal16, seleument le premier terme aussi doit être générer (j'utilise ce terme parce que je doit utilisé cette fonction pour un site web)
il correspond (le premier terme
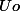
) à une fonction décroissante tel que :
 = F(1) = 2,5)
et
 > F(i+1))
et
 > 0)
pour tout
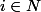
genre un fonction hyperbolique

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 08 Juin 2017, 11:05
par zygomatique » 08 Juin 2017, 11:05
salut
alors on posant
 = F(i + 1) - F(i))
alors
 = F(n) - F(0) < a)
est à variation bornée et tu choisis ce que tu veux pour f : monotone, non monotone, constante (cas d'une suite arithmétique)
par exemple
 = \dfrac k {2^x})
où k est un coefficient de normalisation tel que
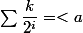
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
ncrroger
- Messages: 5
- Enregistré le: 06 Juin 2017, 14:55
-
 par ncrroger » 08 Juin 2017, 17:44
par ncrroger » 08 Juin 2017, 17:44
Merci @zygomatique pour ta réponse sa me semble être ce que je cherche.
et Merci à tous.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités