Fonction polynome du second degre

[user0m02]

Bonjour, pouvez-vous m'aider s'il vous plait ?

f est une fonction polynôme du second degré définie sur R par f(x)=ax2+bx+c
1. On suppose que a>0
a. Utiliser la forme canonique de f pour démontrer que cette fonction admet un minimum dont on précisera la valeur ainsi que l'antécédent xm pour lequel il est atteint.

b. Montrer que si u et v sont deux nombres réels tels que u<v«xm alors f(u)-f(v)>0. En déduire le sens de variation de f sur ]-∞; xm].
Aide : On se ramènera à étudier le signe de : a x (u-v) x [(v-xm)].

c. Etudier de même le sens de variation de f sur [xm; +∞[.

2. Etudier de même les variations de f lorsque a<0.

[vam]

Bonjour

tu as certainement déjà fait quelque chose, dis le...où en es-tu ?

[user0m02]

Merci pour votre réponse.
oui effectivement j'ai trouvé que f(xm)=β donc f(xm)=-(b²-4ac)/4a
Mais après je n'arrive pas à en déduire xm

Je sais aussi que x=α

[vam]

Bonjour

je pense que cette fiche devrait te donner des idées pour ton exercice
https://www.ilemaths.net/maths_1-factorisation-polynomes-cours.php

[catamat]

Bonjour

Pour le 1)

On a où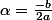

Comme a est positif et le carré également f(x)est supérieur à ce qui permet de conclure.