Salut à tous,
j'ai pu lire sur le net le résultat suivant : Il existe un nombre réel x tel que la suite E(2^2^.....^2^x) ne contienne que des nombres premiers.
Avez-vous une idée de démonstrations ou un lien? Introuvable sur le net...
Exponentiation et nombres premiers
5 messages
- Page 1 sur 1
Ola,
Sans rentrer dans les details, je pense qu'il faut choisir une suite p_k de nombres premiers telle que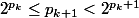 (possible grace au postulat de Bertrand)
(possible grace au postulat de Bertrand)
et que pour une telle suite on peut trouver un reel x tel que pour tout k, p_k\leq 2^2^...^2^x<p_k+1 (en construisant un x qui marche pour les premiers entiers k, puis en affinant de proche en proche la precision de x pour qu'il marche pour les entiers k suivants.. )
Sans rentrer dans les details, je pense qu'il faut choisir une suite p_k de nombres premiers telle que
et que pour une telle suite on peut trouver un reel x tel que pour tout k, p_k\leq 2^2^...^2^x<p_k+1 (en construisant un x qui marche pour les premiers entiers k, puis en affinant de proche en proche la precision de x pour qu'il marche pour les entiers k suivants.. )
Si on connait une majoration simple du nombre de chiffres (en base 10) du nième nombre premier, j'imagine qu'on doit pouvoir bricoler un nombre réel x type Champernowne et une formule avec des parties entières qui donne la suite des nombres premiers au grand complet (mais on tourne encore en rond puisque pour connaitre ce x il faudrait déjà connaitre tous les nombres premiers).
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
