EQUATION DIFFERENTIELLE

[hatimhh]

Bonjour,
dans cet exercice on me demande de montrer que l’équation différentielle (F) : 4U" + U^(2n+1) - U = 0 admet une solution unique, et ensuite déterminer cette solution. Sachant que dans la question précédente (la c'est bon il suffit de remplacer l'equation (F) par sa solution et on trouve que que Y est solution de (E)) on me demande de montrer : Y est solution de l’équation (E) définit par (E) Y" + Y^(2n+1)/(4x^(n+2))=0 <==> U(t)=Y(exp(t))exp(-t/2) est est solution de (F).
je pense qu il faut trouver la solution de l’équation (E) et remplacer Y dans U . Mais je n'arrive pas à l’intégrer.

N.B:( Y et U sont de classe C^2)
Merci d'avance.

[Ben314]

Salut,
Si tu multiplie l'équation par 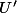, ça s'intègrerais pas de façon assez triviale ton truc ?

[hatimhh]

Salut,
Si tu multiplie l'équation par , ça s'intègrerais pas de façon assez triviale ton truc ?

oui mais je me trouverai face a l' eqt U'^{2} + \frac{U^{2n+2}}{2(n+1)}-\frac{U^{2}}{4}=\frac{C}{2}

[Ben314]

Effectivement, je vois pas bien comment intégrer ça.
Sinon, ce que je comprend pas,c'est ton histoire de solution unique. Tes équations, elles ont évidement une infinité de solutions : si on se donne un xo, et les valeurs de U(xo) et de U'(xo) il va forcément y avoir une unique solution de (F) définie sur un certain voisinage de xo [théorème de Cauchy-Lipschitz]. Pour qu'il y ait une solution unique, il faut soit se donner des valeurs initiales, soit demander à ce que la domaine de définition de la solution soit au moins égal à un certain domaine. Sauf qu'on a ni l'un ni l'autre ici . . .
Après, si tu cherche des solutions "au pif", tu as au moins celles de la forme U(t)=Cst=racine 2n-ième de l'unité qui correspondent à Y(x)=Cst.racine(x) sur ]0,+oo[ (avec toujours Cst=racine 2n-ième de l'unité). Mais bon, rien que ça, ça te fait déjà plusieurs solutions (et il y en a des tonnes d'autres...)