à partir de la forme

on peut considérer deux cas : m pair
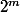
est donc un carré
la résolution de y² = w² + w + 1 conduit à la recherche des diviseurs de 7 donc un nombre fini de solutions, à savoir une seule : w = 1 (ou w = -2 dans Z) et m = 2
en dehors de cette solution, toutes les autres ont donc m impair et w² + w + 1 est le double d'un carré 2y²
ce qui conduit à une équation de Pell (nombre infini de solutions) dans lesquelles il faut pêcher celles pour lesquelles y est une puissance de 2,
mais bon , ça n'avance pas trop...
sauf qu'on sait maintenant que m est impair pour les autres solutions que w = 1, m = 2
les solutions de 2y² = w² + w + 2 sont obtenues par la récurrence


en partant de
)
=
(0, -1) :
(-3, -2) (-16, -11)
(-91, -64) (-528, -373) (-3075, -2174) (-17920, -12671) ...
(-1, -1) :
(-6, -4) (-33, -23) (-190, -134) (-1105, -781) (-6438, -4552) (-37521, -26531) ...
(-1, 1) :
(2, 2) (15, 11)
(90, 64) (527, 373) (3074, 2174) (17919, 12671) (104442, 73852) ...
et (-3, 2) : (0, 1)
(5, 4) (32, 23) (189, 134) (1104, 781) (6437, 4552) (37520, 26531) ...
dans lesquelles j'ai souligné les solutions où |y| est une puissance de 2
on retrouve les 4 solutions déja connues avec w > 0 (en comptant le cas y² = w² + w + 1 au dessus)
bien entendu aller comme ça jusqu'à l'infini n'est pas possible, mais c'est du même genre que d'autres problèmes qui aboutissent à filtrer des solutions définies par des récurrences du second ordre (solutions d'équations de Pell)
il est "bien rare" qu'il y ait parmi ces solutions un nombre infini de solutions qui satisfasse à un quelconque critère additionnel (ici que ce soit une puissance de 2)
les démonstrations sont souvent très tordues ... et très longues
