Diverses preuves de l'irrationnalité de √2
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 15 Nov 2008, 22:04
par leon1789 » 15 Nov 2008, 22:04
oui, c'est une preuve n'utilisant pas la divisibilité de Z.
Zweig a écrit: Donc

est vide.
Il faut éviter 0 dans E ->
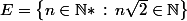
.
Zweig a écrit:En particulier, lorsque
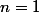
, on montre l'incommensurabilité de

.
avec n=1, on montre (seulement) que
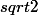
n'est pas entier.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 15 Nov 2008, 22:17
par Zweig » 15 Nov 2008, 22:17
Oui, j'ai conclu un peu trop vite. Pour montrer qu'il est irrationnel, il faut considérer
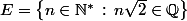
.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 15 Nov 2008, 22:33
par Zweig » 15 Nov 2008, 22:33
Pour l'irationnalité de
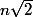
, il suffit de considérer
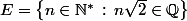
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 16 Nov 2008, 12:15
par acoustica » 16 Nov 2008, 12:15
Zweig, tes fiches pdf come celle-là, tu les met sur un blog? Si oui quelle est l'adresse?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 26 Avr 2009, 10:05
par leon1789 » 26 Avr 2009, 10:05
Voici une petite preuve donnant une minoration de
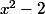
pour
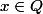
.
Soit
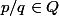
. On écrit
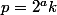
et
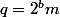
où k et m sont impairs. On a
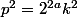
et
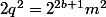
Si
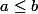
alors on a
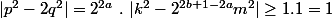
car
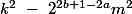
est impair (
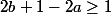
).
Si
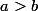
alors on a
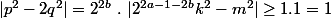
car
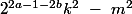
est impair (
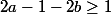
).
Dans tous les cas,

d'où
^2 - 2| \geq 1/q^2)
,
ce qui démontre en particulier que
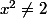
pour tout
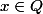
.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 26 Avr 2009, 11:27
par leon1789 » 26 Avr 2009, 11:27
:++: Et sur
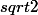
?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Avr 2009, 11:48
par Joker62 » 26 Avr 2009, 11:48
Y'a pas d'article dessus :D
Par contre y'en a vraiment des pas mal.
Comme par exemple les espèce de Bananach qui sont dit Split lorsqu'il sont jaunes :D
-
SimonB
 par SimonB » 26 Avr 2009, 11:51
par SimonB » 26 Avr 2009, 11:51
La preuve de leon fait un peu penser aux inégalités obtenues pour montrer la transcendance de certains nombres. (S'il faut vraiment que je précise ce que je dis, dites-le, j'irai chercher des références...)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 07 Mai 2009, 07:31
par leon1789 » 07 Mai 2009, 07:31
On peut refaire une preuve similaire en utilisant l'écriture
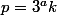
et
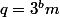
où k et m ne sont pas multiples de 3. Mais cela n'apporte rien de plus que
^2-2| \geq 1/q^2)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
est vide.
, on montre l'incommensurabilité de
.