Tiens, j'ai trouvé une solution à ton exo le_chat :
On peut montrer que l'on peut définir une loi de groupe sur
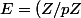^2)
privé de
 | x^2+y^2=0})
par
.(u,v) = (xu-yv,xv+yu))
Alors l'ensemble

que l'on cherche est un sous groupe de E et donc divise son cardinal.
Il suffit de determiner le cardinal de
 | x^2+y^2=0})
On a d'abord la solution
)
.
Ensuite, si on tient un élement
)
avec x et y différent de 0, alors
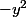
est un carré soit
^{((p-1)/2)} * y^{p-1} = 1)
soit
/2)
est pair soit

divisible par 4.
Ainsi :
Si

est divisible par 4, étant donné un y non nul, l'équation
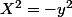
admet une solution, et donc 2.
Donc le cardinal recherché est
=2p-1)
.
Si

n'est pas divisible par 4, alors le cardinal est de 1.
Ainsi, si

non divisible par 4 : card F divise
(p+1))
soit Card F =1 ou

ou
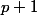
ou
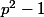
.
Sinon card F divise
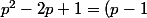^2)
soit card F = 1,

ou
^2)
Mais, on montre aussi que 4 divise card F.
En effet, si on réalise une partition de

par (en identifiant classe d'équivalence et élément de [|1;n|]) :
 \in F | x \leq (p-1)/2 , y \leq (p-1)/2 })
 \in F | x \geq (p-1)/2 , y \geq (p-1)/2 })
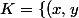 \in F | x \leq (p-1)/2 , y \geq(p-1)/2 })
 \in F | x \geq (p-1)/2 , y \leq (p-1)/2 })
Alors les involutions
 -> (-x,-y))
;
-> (x,-y))
;
 -> (-x,-y))
envoient

respectivement sur

,

et

.
Donc card F = 4 card I.
On peut montrer facilement que card F <=
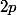
(Etant donné x, il ne peut y avoir au maximum que deux y tel que x²+y²=1)
Ainsi : si 4 ne divise pas

, card F ne peut valoir que
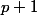
(le seul divisible par 4)
sinon card F =

.
Au final,
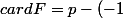^{\frac{p-1}{2}})
.
Mais je soupconne plus court ... :marteau:
.
.
premier.
?
tel que :