Demontstration (A\B)\(B\C)=A\(BuC)

[Jatrigrn]

Bonjour,
Je dois démonter (A\B)\(B\C)=A\(BuC) mais je n'y arrive pas.
Est-ce que quelqu'un pourrait m'expliquer la démonstration?
mercii

[hdci]

Bonjour,
J'imagine que BuC c'est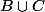 . Pour t'aider, voici ce qu'il faut taper entre les deux balises "Tex" qui apparaissent quand tu cliques sur le bouton "tex" juste à côté de "Couleur de la police" :
(A\setminus B)\setminus (B\setminus C)=A\setminus (B\cup C)

Ce qui donne (c'est plus lisible...)


Deux choses :

• Je pense par ailleurs qu'il y a une erreur d'énoncé. Ne serait-ce pas plutôt ceci ?
  
  
  En effet, si on prend alors et ...
  
  
• Pour démontrer cela : quelle méthode connais-tu, généralement, pour démontrer que l'ensemble est égal à l'ensemble ?
  
  Tu peux également t'appuyer sur une figure : en as-tu fait une ? de type "diagramme de Venn" (ce sont des "ronds ou ovales" qui représentent les ensembles, avec leurs intersection, etc.) ; si tu fais 3 "patates" qui s'entrecroisent (une pour A, une pour B, une pour C) et que tu "colories" les différents éléments, tu peux "voir" le résultat et en déduire ce qu'il faut faire pour démontrer l'égalité.