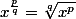Demonstration (exposant rationnel)

[maxence6]

Bonjour,
Suite au post "Racine n ième, n Décimal ? " de Lostounet je relance le sujet mais vers une autre direction, la démonstration de ces propriétés suivantes !

Pour ceux qui ne l'on pas vu, on été parti sur:



et



Mais moi je veux savoir d'où ça vient !
Donc s'il vous plait éssayé de faire ou d'éssayé de faire la démonstration,

Merci d'avance et bonne chance ! :ptdr:

[Lostounet]

Oui moi aussi tiens ! Ce serait intéressant :D

[maxence6]

J'espère que c'est intéressant enfin plutôt que ça va vous intéresser ! :happy2:

[AL-kashi23]

Bonsoir!

Pas lu l'autre post mais ce n'est ici qu'affaires de notations il me semble.

Pourquoi pas 3$2 pour dire 3 fois 2 ? Conventions!

[Lostounet]

Bonsoir!

Pas lu l'autre post mais ce n'est ici qu'affaires de notations il me semble.

Pourquoi pas 3$2 pour dire 3 fois 2 ? Conventions!

Comment ça?

Il est plus question d'un: "Pourquoi est-ce que 5/2 = 5 * 0,5"
Et non d'un pourquoi on note 5 * 0,5 pour le produit de 5 par 0.5 :marteau:
Donc pourquoi est-ce qu'on se permet cette égalité ? Par quel équilibre cosmique fonctionne-t-elle ?

[maxence6]

Ca a l'aire d'intéresser que nous Lostounet !

[Lostounet]

Ca a l'aire d'intéresser que nous Lostounet !

Meuh non, attendons un peu, je suis sûr qu'il y aura du retour prochainement, d'ici demain au pire! Le forum ne manque ni de vie, ni de niveau :we:

[Ben314]

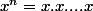
Au dépar, tout part de la notation (n fois) qui n'a évidement du sens que pour n entier supérieur ou égal à 1 (et x réel ou complexe ou... quelconque).
Il est facile de montrer que, pour n et m entiers supérieurs ou égaux à 1, on a :
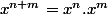
et
On veut ensuite étendre cette notation à n=0, puis n<0, puis n rationel, mais on aimerais que les formules ci dessus restent vrais.
Dans la première formule, si on prend m=0, on constate que, pour que la formule soit valable, il faut définir 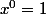: c'est donc bien une définition (i.e. cela ne se démontre pas) MAIS cette définition n'est absolument pas tirée au hasard !!!
Ensuite, toujours la même formule où l'on prend m=-n montre que, si l'on veut que la formule reste vrai, on doit définir .
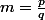
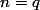
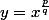
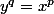
On utilise ensuite la deuxième formule avec et pour voir que, si l'on veut définir , on doit choisir un tel que , c'est à dire définir

[alavacommejetepousse]

bonsoir
une simple remarque
les fonctions racines n ièmes et puissances fractionnaires ne coïncident que sur R +*

[maxence6]

Heureusement que t'es là Ben314 :happy2:

[Cym13]

il y a plus simple lorsqu'on est familiarisé avec les logarithmes :

partons de qui devient

multiplier c'est diviser par l'inverse donc et donc .
En passant à l'exponentielle on obtiens bien l'égalitée recherchée :.


Le même type de raisonnement s'applique dans la résolution de la seconde démonstration qui s'appuie sur le fait (évident) que : de sorte que : .
Un passage à l'exponentielle donne la seconde égalité.


Les logarithmes sont plus durs à orthographier qu'a apprendre, je conseille en fait plutôt les videos de cours car tu pourrais ne pas saisir le sens des textes (c'est à mon sens une opération plutôt visuelle mais tu fait comme tu veux).

Désolé si je n'ai pas été très clair, c'est mon premier post :we:

[maxence6]

Moi si je veux prouvé que je m'y prend de cette façon:

[Lostounet]

On ne peut prouver une propriété avec des exemples numériques :s

[maxence6]

Tout à fait mais il suffit d'un peu de bon sens ^^