Ici, tes deux "formules" ne sont pas des distances sur R^3, mais uniquement sur
des parties de R^3 : sur la sphère x²+y²+z²=R² pour la première et sur l'hyperboloïde de révolution -x²-y²+z²=R² pour la seconde.
Dans les deux cas, si tu cherchait la "métrique locale" en étudiant la limite lorsque
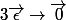
de
)
où
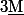et 
sont des points de la surface ben tu tomberais sur... la métrique usuelle de R^3 vu qu'on est parti de celle là pour calculer les distances géodésique sur la surface...
Si tu veut trouver des métriques interessantes, il faut que tu paramétrise tes surfaces à l'aide d'une fonction définie sur R^2 (ou une partie de R^2).
Ensuite, la métrique "usuelle" sur R^3 définie naturellement une métrique sur la surface contenue dans R^3 et, ta paramétrisation te permet de définir maintenant une métrique sur la partie de R^2 que tu as utilisé pour paramétrer (métrique qui
n'est pas la métrique usuelle de R^2).
Evidement, la métrique que tu obtient dépend de la paramétrisation choisie, mais tout aussi évidement, les propriété "géométriques" de ta métrique ne dépendent pas de la paramétrisation.
