Montrer que :
* Déterminer un équivalent de
De la convergence en somme d'intégrale
2 messages
- Page 1 sur 1
De la convergence en somme d'intégrale
par Elerinna » 13 Mar 2012, 23:23
* Préliminaire. Soit )
décroissante et telle que : dt)
converge.
Montrer que :)
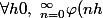converge et déterminer : )
* Déterminer un équivalent de
quand 
tend vers 0 par valeurs supérieures.
Montrer que :
* Déterminer un équivalent de
par girdav » 18 Mar 2012, 22:44
Bonjour,
il faut découper :dt=\sum_{n=0}^{+\infty} \int_{nh}^{(n+1)h}\varphi(t)dt\geq \sum_{n=0}^{+\infty}h\varphi((n+1)h))
d'où la convergence de la série. On a
h)\leq \int_{nh}^{(n+1)h}\varphi(t)dt\leq h\varphi(nh))
donc
dt\leq h\sum_{n=0}^{+\infty}\varphi(kh)\leq h\int_0^h\varphi(t)dt+\int_0^{+\infty}\varphi(t)dt)
d'où =\int_0^{+\infty}\varphi(t)dt)
.
il faut découper :
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :