Le titre du fil de discussion est:
CONNAÎTRE CANTOR, SON OEUVRE, SA PERSONNALITÉ
ben moi je vois le mot personnalité
donc je trouve légitime mes réponses non maths sur :
-Lacan
-la question non répondue de lazare:
"Le livre parle t'il de ce qui motivait Cantor a checher sa theorie des enssemble et etudier l'infini ?"
Sur l'aspect purement mathématique il était possible à GBZM de parler de Cantor dans le fil de discussion de Spalding, fil de discussion où GBZM n'a fait que parler de l'arrondi de Spalding.
Connaître Cantor, son oeuvre, sa personnalité
27 messages
- Page 2 sur 2 - 1, 2
Re: Connaître Cantor, son oeuvre, sa personnalité
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Connaître Cantor, son oeuvre, sa personnalité
Et pour ceux que cela intéresse ils peuvent lire les lettres de Cantor à son ami mathématicien,
c'est un grand moment de l'histoire des sciences,
un grand moment de l'apparition des idées
tapez dans google: Cantor lettre à son ami mathématicien
c'est un grand moment de l'histoire des sciences,
un grand moment de l'apparition des idées
tapez dans google: Cantor lettre à son ami mathématicien
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Connaître Cantor, son oeuvre, sa personnalité
Pas retrouvé la (les) lettre de Cantor à Dedekind.
en cherchant cette lettre je suis tombé sur ce résumé sympa, non?:
https://irem.univ-amu.fr/sites/irem.uni ... 5mn-v2.pdf
"Je le vois mais je ne le crois pas"
un peu de Dedekind Cantor ici:
https://www.lpsm.paris/pageperso/mazlia ... _cours.pdf
en cherchant cette lettre je suis tombé sur ce résumé sympa, non?:
https://irem.univ-amu.fr/sites/irem.uni ... 5mn-v2.pdf
"Je le vois mais je ne le crois pas"
un peu de Dedekind Cantor ici:
https://www.lpsm.paris/pageperso/mazlia ... _cours.pdf
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Connaître Cantor, son oeuvre, sa personnalité
Quelques formules
=\aleph _0)
=\aleph _0)
=\aleph _1)
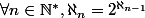
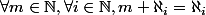
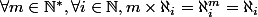
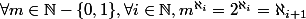
L'hypothèse du continue stipule qu'il n'existe pas de transfini tel que
tel que
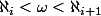
Cette hypothèse est indécidable dans ZF
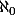 est appelé la puissance du dénombrable
est appelé la puissance du dénombrable
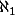 est appelé la puissance du continu
est appelé la puissance du continu
L'hypothèse du continue stipule qu'il n'existe pas de transfini
Cette hypothèse est indécidable dans ZF
Re: Connaître Cantor, son oeuvre, sa personnalité
Bonjour,
Comme l' a écrit GBZM,les alephs ne sont pas indicés par N mais par les ordinaux.
Comme l' a écrit GBZM,les alephs ne sont pas indicés par N mais par les ordinaux.
Re: Connaître Cantor, son oeuvre, sa personnalité
azf a écrit:
Non, ce n'est pas la définition de
Non
Non
L'hypothèse du continue stipule qu'il n'existe pas de transfinitel que
Non
est appelé la puissance du continu
Non.
azf, s'il te plaît, évite d'intervenir à tort et à travers.
27 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
