Je me lance dans une tentative de démonstration pour le cas
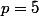
et
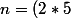^{2^{a+1}.5^b}+1)
*****************
Démonstration
*****************
Etape 1 : Montrons que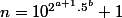 
est 
-probablement-premierUn nombre entier naturel
est
-probablement-premier ssi
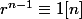
est premier avec
1-1/ Mq 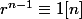Posons
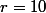
et
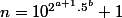
avec
et
des entiers naturels.
Notons
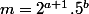
, il vient :
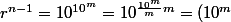^{\frac{10^m}{m}}=(10^m)^{\frac{2^m.5^m}{m}}=(10^m)^{\frac{2^m.5^m}{{2^{a+1}5^b}}}=(10^m)^{2^{m-a-1}.5^{m-b}}=(10^m)^{2.(2^{m-a-2}.5^{m-b})}=(10^m)^{2.K}\equiv (-1)^{2.K}[10^m+1]\equiv 1 [10^m+1])
avec
un entier naturel qui existe pour toutes valeurs de
et
.
1-2/ Mq est premier avec Si
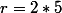
divise
alors
est divisible par
ou par
or
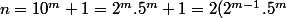+1)
est un entier impair donc non divisible par
.
D'autre part,
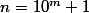
est un entier qui ne se termine jamais par
donc il n'est pas divisible par
.
1-3/ Conclusion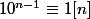
et
est premier avec
donc
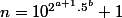
est
-probablement-premier pour tout entier naurel
et
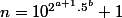Etape 2 : Montrons que est -fortement-probablement-premierUn nombre entier naturel
est
-fortement-probablement-premier ssi
(1) En écrivant
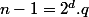
avec
impair et
entier, on a
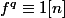
ou (2) s'il existe un entier
compris entre
et
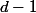
tel que
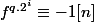2-1/ Mq 
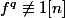(1) n'est jamais vraiePosons
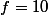
et rappelons que
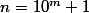
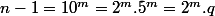
avec
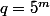
impair, il vient
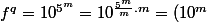^{\frac{5^m}{2^{a+1}.5^b}}=(10^m)^{\frac{5^{m-b}}{2^{a+1}}}=(10^m)^{K'}\equiv (-1)^{K'} [n])
mais
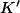
n'est pas un entier donc
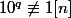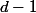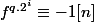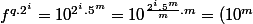2-2/ Mq il existe toujours un entier compris entre et tel que (2) est toujours vraie^{\frac{2^i.5^m}{2^{a+1}.5^b}}=(10^m)^{2^{i-a-1}.5^{m-b}}\equiv (-1)^{K"}[n]\equiv -1 [n])
si
![](https://latex.ilemaths.net/ile_TEX.cgi?K")
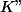
est impair or
![](https://latex.ilemaths.net/ile_TEX.cgi?K"=2^{i-a-1}.5^{m-b})
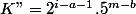
n'est pas divisible par
si
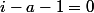
. Cette condition est assurée lorsque
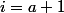
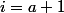
est positif pour tout entier naturel
De plus,
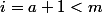
et rappelons que
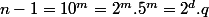
avec
impair
Par identification,
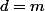
et nous venons de voir que
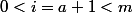
donc
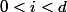2-3/ ConclusionTout entier naturel de la forme
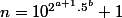
est
-probablement-premier et
-fortement-probablement-premier
