La conjecture la plus robuste ébranlée par un contre exemple

[anthony_unac]

Bonsoir,
Quelle est selon vous la conjecture la plus robuste qui ait été ébranlée par un simple contre exemple ?

[Lostounet]

Bonsoir,
Quelle est selon vous la conjecture la plus robuste qui ait été ébranlée par un simple contre exemple ?

Que penses-tu de:

[anthony_unac]

Joli coup Lostounet et du coup le pauvre Euler est mort sans la prendre dans la gueule celle la

Je te propose celle ci dans le même registre (le registre des entiers parce que ça me fait ...) :

Pour tout entier n :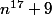 et sont premiers entre eux.

Jean Paul Delahaye p.191(tiens donc un nombre premier) du livre "Merveilleux nombres premiers" écrit concernant cette conjecture :
" Vous pouvez vérifier cela jusqu'à 100, 1000, un milliard [...], et même jusqu'à 8 millions de milliards de milliards de milliards de milliards de milliards ().
Pourtant, un peu plus loin, vous trouverez une exception pour :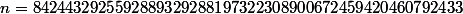
En conclusion, les nombres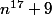 et ont parfois des facteurs communs."

[Lostounet]

C'est bizarre mais beau?
Je n'ai pas le courage de vérifier...

Pourquoi 17 et 9...?