Cantor-Bernstein.

[Pafapafadidel]

Si il existe une injection d'un ensemble A dans un ensemble B, alors A est en bijection avec un sous-ensemble de B et donc card(A) est inférieur ou égal a card(B).
Si de plus il existe une injection de B dans A, alors B est en bijection avec un sous-ensemble de A et donc card(B) est inférieur ou égal a card(A).
On a donc card(A)=card(B), et il existe donc bien une bijection entre A et B, ce qui démontre le theoreme de Cantor-Bernstein.

Ce raisonnement est clairement faux, la véritable démonstration étant légerement plus compliquée, mais pourquoi? Ou est l'erreur?

[Ben314]

Salut,
Il y a deux "façons" de voir l'erreur dans ce raisonnement : cela dépend du sens que tu donne à la phrase "card(A) est inférieur à card(B)"

1) Soit tu définis
"card(A) est inférieur à card(B)" "il existe une injection de A dans B"
et dans ce cas, il faut DEMONTRER que [ card(A) inf. à card(B) ET card(B)inf. à card(A) ] => card(B)=card(A). c'est à dire qu'il faut avoir démontré Cantor-Bernstein pour que ton raisonnement soit vrai.

2) Soit tu définis "card(A)" comme étant un élément de "la classe des cardinaux" (que tu doit définir et qui n'est pas un ensemble...) et, dans ce cas, pour que ton raisonnement soit valable, il faut montrer que l'on peut munir la classe des cardinaux d'une relation d'ordre.
En particulier, il faut vérifier l'antisymétrie de la relation d'ordre, c'est à dire démontrer Cantor-Bernstein...

Conclusion : ton raisonement est parfaitement valable, mais il faut absoluement avoir démontrer Cantor-Bernstein AVANT pour le justifier.....

P.S. A la rigueur, en utilisant le deuxième point de vue et uniquement des ensembles finis, la "classe des cardinaux" devient l'ensemble N et, dans ce cas, on peut montrer l'antisymétrie sans Cantor-Bernstein (on fait plus ou moins une récurrence...)

[Finrod]

Mais pour des ensembles finis, c'est évident non ? comme pour des esp vect finis.

[Ben314]

Mais pour des ensembles finis, c'est évident non ? comme pour des esp vect finis.

Tout dépend de ce que tu appelle une "évidence"...

Le résultat qu'il faut montrer est que, si un ensemble A est en bijection avec l'ensemble {1,2,...,n} et aussi avec l'ensemble {1,2,...,m} alors n=m.

C'est une "évidence" dans le sens qu'un enfant qui apprend à compter des objets trouve normal que le nombre d'objets compté ne dépend pas de l'ordre dans lequel il les a compté (d'ailleur,à mon avis, il ne se pose pas la question !!!)

Par contre, si tu est matheux et féru de logique, ce résultat n'étant pas dans les axiomes de Péano (ni de ZF)... il faut bien le démontrer (par récurrence)

P.S. Pour montrer qu'il y a bien "quelque chose à démontrer", je rajouterais que sur Q ou R, le résultat est faux : [0,a] en bijection avec [0,b] n'implique pas que a=b...

[Finrod]

En gros on est en train de montrer que f injective pour des ensemble fini implique que le cardinal de départ est plus petit que le cardinal d'arrivé.

et pour cela on doit montrer que le card de l'espace de départ est égal au cardinal de son image (ce que tu proposes).

Comme preuve sans récurrence, je pensais à

n et m jouant des rôles symétriques, on peut supposer n plus petit que m sans perte de généralité.

Soit f:de [1,n] dans [1,m] qui réalise la bijection. Quitte à composer par un élément de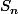 , on peut supposer que f envoi i sur i.

Maintenant, si m>n, alors m n'a pas d'antécédent et f n'est pas une bijection. C'est la contraposé de ce que l'on veut montrer. Donc Si f est bijective, m=n.

Bon évidemment, au moment ou je parle de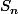 , il y a peut être une petite récurrence cachée...

[Ben314]

Bon évidemment, au moment ou je parle de , il y a peut être une petite récurrence cachée...

Il me semble bien que oui : comment définit tu ton élément g de Sn tel que fog(i)=i pour tout i dans {1..n} ?
Evidement, il est interdit de dire g=f^(-1) et de dire... c'est évident.

En fait, ce résultat est valable pour tout ensemble bien ordonné et il me semble qu'on ne peut pas se passer du bon ordre (i.e. de la réccurence)

Edit : Vérifie bien que ta preuve n'est pas valable si [1,n] et [1,m] sont des intervales de R ou de Q car dans ce cas, le résultat est faux.
Il faut donc nécéssairement utiliser quelque chose de vrai dans N et faux dans Q et R...

[Finrod]

Les intervalles ne sont pas des ensembles finis.

Et oui, en fait, j'ai pas fait gaffe mais j'ai fait le cas ordonné.

Mais bon, avec l'axiome du choix, je pense qu'on peut s'en sortir aussi dans le cas non ordonné.

Edit: en ait sur des ensembles finis, je pense qu'on peut ajouter artificiellement une structure d'ordre. Cela ne change pas l'ensemble sous-jacent et la bijection n'est pas supposé "respectant l'ordre" à la base.