jreviens à la charge :hum:
Toujours avec notre centre X. Nous allons dire que cette fois, c'est le centre, repéré par (0,0).
On prends les hauteurs h_a,...,h_f, qui sont les distances des segments qui partent de X et sont perpendiculaires aux cotés (resp) a,...f.
On s'intéresse qu'au côté a.
On peut exprimer lexpression de la droite qui mene a en fonction de h_a et un angle que nous nommons theta_a. On nomme cette droite (d_a)
Comme c'est un polygone, nous avons une intersection entre (d_a) et (d_b) que nous pouvons exprimer en fonction de h_a,h_b, theta_a et theta_b
Au final, en joingnant deux droites en un point commun a chaque fois, on obtient un systeme dequation.
Si le polygone a 6 coté : on a 6 angle, 6 points d'intersections, donc si equations a 6 inconnues.
Voila comment determiner lequation de (d_a)en fonction de y et x (au lieu de r et theta)

Bon,...,
le truc bleu c'est le coté a.
On a tracé [XH] avec XH= h_a, et H projeté orthogonal de (XH) sur (d_a)
Le but c'est de trouver y_a = ax_a+b, qui satisfait l'angle theta_a et r.
le coeff a est donné par theta_a.
Pour determiner le coeff b on peut chercher lordonnee a lorigine :
On determine X'X:
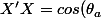*h_a)
Pour le ptit bout manquant, (jor l'intersection de (XX') avec (d_a) que jnomme X") X'X", on peut calculer X'H puis rebelotte.
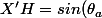*h_a)
d'ou
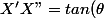X'H)
Soit
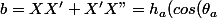+\frac{sin^2(\theta_a)}{cos(\theta_a)}))
Bon, sauf erreur, bien sûr...


