Arithmétique : une inégalité "classique" ?

[Nicolas.L]

Bonjour,
C'est la première fois que je poste sur ce forum, je m'excuse si mon sujet n'est pas à sa place.

Dans l'un de mes livres, l'auteur utilise un résultat qui selon-lui "se montre facilement par récurrence", il affirme que, si est un entier strictement positif alors

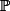
( où est l'ensemble des nombres premiers)

J'ai essayé mais je ne vois pas comment montrer ce résultat.. auriez vous une piste ?

[jlb]

salut, oui!! par récurrence, essaie de commencer, je te donnerai des indications au fur et à mesure.
initialisation: pour n=2
hérédité: suppose la propriété vrai jusqu'au rang n, et regarde ce qu'il se passe si n+1 est impair (facile)puis le cas où n+1 est pair qui est plus délicat ( il faut découper le produit astucieusement de p=2 à k+1 et de p=k+2 à 2k+1=n+2).

bon courage, j'ai peut-être écrit des bêtises sur les indices, il est tard.

[Nicolas.L]

Salut, je n'ai réussi à aller beaucoup plus loin que ce que tu me propose..

Le cas où n+1 est impair ne pose effectivement pas de problème puisque alors n+2 est pair et ne peut pas être premier. (donc le produit ne change pas)

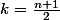
Dans le cas ou n+1 est pair j'ai essayé comme tu l'a proposer de poser et d'écrire



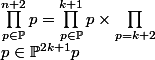
Par hypothèse de récurence on a Mais je ne sais pas quoi faire du deuxième facteur :triste:

Je remarque d'ailleurs que je n'arrive pas à construire un argument basé sur le fait que les p sont premiers...

[jlb]

impeccable, on passe alors au chose sérieuse!!!

Il reste à majorer la partie restante, accroche-toi!!

Ce qui reste peut s'écrire à partir d'une combinaison de k+1 termes parmi 2k+1 et d'un facteur adéquate, tu vois comment?
Je te laisse chercher après il restera à montrer que tous les premiers du produit divisent cette expression et le tour sera presque joué. Je te laisse réfléchir à cela, je pars au boulot. Bon courage, je te donne la suite ce soir.

[Nicolas.L]

J'ai peut être une idée se solution..

On peut dire que le deuxième facteur vaut " (k+2)(k+3)...(2k+1) divisé par tout les nombres non premier de l'intervalle [k+2;2k+1] "

Or
de plus, pour il existe un multiple de dans l'intervalle [k+2;2k+1]. On peut donc écrire



Or on a

et

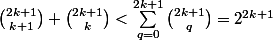
Ce qui donne



Qui donne l'inégalité souhaitée :zen:

Merci pour ton aide !