Arithmétique

[Wilfried]

Bonjour
Si on considère deux entiers naturels a et b, peut-on trouver à quelles conditions sur le couple (a,b) le chiffre b²(1-a)² + 4b est un carré ?

Merci d'avance.

[WillyCagnes]

bonjour,

regarde pour a*b=1

[lyceen95]

Je préfère écrire b²(a-1)²+4b , je n'aime pas les nombres négatifs.
Si a = 1, cette expression donne 4b. C'est un carré dès que b est un carré.
Si a est plus grand que 2, on constate que cette expression est comprise entre ( b(a-1) )² et ( b(a-1) +1)² , donc pas un carré.
Si a vaut 2, c'est un peu plus compliqué à encadrer entre 2 carrés consécutifs, mais ce n'est pas un carré non plus

[Ben314]

Salut,
Il y a aussi le cas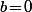 (et quelconque) qui marche.

P.S. : à moins que 0 ne soit plus considéré comme un entier naturel : vu l'évolution des conventions vers celles, assez souvent débiles, des anglo-saxons, je me méfie . . .